Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 01. 2010 17:00
Geometricky priklad
Na prepone AB pravouhlého rovnoramenného trojuholníka ABC sú dané také body M a K (K je medzi M, B), že veľkosť uhla MCK je 45°. Dokážte, že |MK|^2=|AM|^2+|KB|^2
Mohli by ste mi dat nejaku radu? Thanx.
Offline
- (téma jako vyřešené označil(a) Lancer)
#2 18. 01. 2010 19:16 — Editoval FailED (18. 01. 2010 19:19)
Re: Geometricky priklad
Nenapadá mně nic lepšího než vyjádřit si ty úseky přes sinovou větu a potom upravovat takovouhle zrůdnost. Snad někdo přijde s lepším řešením.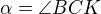 ,
,  je odvěsna.
je odvěsna.
Offline

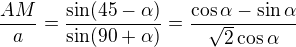
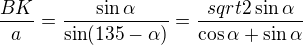
![kopírovat do textarea $AM^2+BK^2=a^2\left[\frac{(\cos\alpha-\sin\alpha)^2}{2\cos^2\alpha}+\frac{2\sin^2\alpha}{(\cos\alpha+\sin\alpha)^2}\right]=\frac{a^2}{2\cos^2\alpha(\cos\alpha+\sin\alpha)^2}$](/mathtex/47/478ef3bee524e6b6d421bcd649f0e0af.gif)
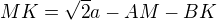
![kopírovat do textarea $MK=a\left[\sqrt2-\frac{\cos\alpha-\sin\alpha}{\sqrt2\cos\alpha}-\frac{sqrt2\sin\alpha}{\cos\alpha+\sin\alpha}\right]=a\left[\frac{2\cos^2\alpha+2\cos\alpha\sin\alpha-\cos^2\alpha+\sin^2\alpha-2\cos\alpha\sin\alpha}{\sqrt2\cos\alpha(\cos\alpha+\sin\alpha)}\right]=\frac{a}{\sqrt2\cos\alpha(\cos\alpha+\sin\alpha)}$](/mathtex/0f/0f6a96856bbfcb6f6266e11fbd554812.gif)
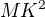 je jasné
je jasné