Matematické Fórum

karlherbert · 19. 01. 2010 17:02

urcete pocet vsech ruznych sesticifernych cisel obsahujici pouze liche cifry jsem se nejak u toho zasekl...

oo · 19. 01. 2010 17:06

variace s opakovanim 6 tridy z (1, 3, 5, 7, 9) 5 prvku?

Jan Jícha · 19. 01. 2010 17:07

Lichá čísla : 1,3,5,7,9
takže $n=5$
Na pořadí prvků záleží, prvky se mohou opakovat. Uspořádáváme to do k-tic, kde $k=6$

holcina.16 · 20. 01. 2010 11:00

V krouzku prvni pomoci pracuje 12 divek a 4 chlapci. Kolika zpusoby muze nastoupit sesticlenne druzstvo,maji-li v nem byt prave dva chlapci. Kolika zpusoby mohou nastoupit,maji-li stat vsechny divky vedle sebe a oba chlapci take?

zdenek1 · 20. 01. 2010 12:58

↑ holcina.16:
1. Tady mi není úplně jasné, co to je "nastoupit". Pokud by to bylo "kolika způsoby můžeme vybrat", pak
Musím vybrat 2 kluky ze 4. To lze 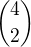${4\choose2}$ způsoby
potom musím vybrat 4 holky ze 12 ${12\choose4}$ způsoby
Výběry jsou nezávislé, takže celkový počet je ${4\choose2}{12\choose4}$ různých družstev

Pokud by to bylo, že už mám vybrané družstvo, a ono nastoupí do řady, pak 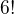$6!$

Pokud by to bylo, že nejprve vyberu družstvo a ono pak nastoupí do řady, tak musíš oba předchozí postupy zkombinovat $6!{4\choose2}{12\choose4}$

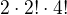2. Jenom kluci můžou nastoupit $2!$ způsoby, jenom holky $4!$ způsoby a můžou stát v pořadí kluci-holky nebo holky-kluci. Takže je $2\cdot2!\cdot4!$ možností (ale zase když už máš družstvo vybrané)