Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Úloha bez ročného obdobia (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 01. 2010 21:06 — Editoval lukaszh (21. 01. 2010 21:15)
Úloha bez ročného obdobia
Ahojte,
na jednej zo starších pokročilejších olympiád sa vyskytla úloha
------------------------------
"Nech X je ľubovoľná množina a nech f: X->X je bijekcia. Ukážte, že existujú zobrazenia g1, g2 také, že f=g1○g2 a g1○g1=g2○g2=id, kde id označuje identické zobrazenie na X."
Nečakajte ohodnotenie z mojej strany (nevyriešil som), pretože skôr by ma zaujímalo ako by ste toto riešili.
EDIT: g1, g2: X->X
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
- (téma jako vyřešené označil(a) byk7)
#2 21. 01. 2010 22:35
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Úloha bez ročného obdobia
↑ lukaszh: Je to úloha pro střední školu?
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Úloha bez ročného obdobia (TOTO TÉMA JE VYŘEŠENÉ)

 lze rozložit na oboustraně nekončné řetězy a konečné cykly a ukázat, že pro každý cyklus i řetěz najdeme involuci
lze rozložit na oboustraně nekončné řetězy a konečné cykly a ukázat, že pro každý cyklus i řetěz najdeme involuci  takovou, že
takovou, že 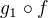 je také involuce.
je také involuce.