Matematické Fórum

marnes · 21. 01. 2010 20:06

Dobrý večer. Chci Vás požádat o pomoc při řešení příkladu výpočtu délky křivky funkce y= lnx v intervalu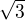
$\sqrt3$ až $\sqrt8$

Meze jsou jasné
Délka křivky je dle předpisu $l=\sqrt{1+(f^,(x))^2}$ po dosazení derivace

$l=\sqrt{1+(\frac{1}{x})^2}$ a nejde mi vypočítat ten integrál - nic mě nenapadá.

Děkuji za jakoukoliv radu

stenly · 21. 01. 2010 20:28

↑ marnes:Integruješ po úpravě funkci (x^2+1)^1/2 /x,slovy integrál odmocniny(x^2+1) lomeno x dx.Zavedeš si substituci :x^2+1=t,pak 2xdx=dt a z toho dx=dt/2x a rovněž x^2=t-1 .Dosadíš do integrálu a int. s proměnnou t .ale musíš změnit meze od 4 do 9!!
Stenly

stenly · 21. 01. 2010 20:33

Lepší bude,když si zvolíš substituci:X^2+1=t^2,pak 2xdx=2tdt a dx=dt/x a rovněž x^2=t^2-1 a dosadíš nové meze 4,9.
Stenly

stenly · 21. 01. 2010 20:37

↑ stenly:Budeš mít integrál 1/2*Int.t^2/(t^2-1) dt meze od 4 do 9!Uděláš fintu v čitateli :t^2-1+1 a pak daný zlomek roztrhneš na dva parciální zlomky a to už je jednoduché!!
Stačí ti to tak polopatisticky??? Stenly

marnes · 21. 01. 2010 20:47

↑ stenly:Dle tvého návodu

X^2+1=t^2,pak 2xdx=2tdt a dx=dt/x a rovněž x^2=t^2-1

$l=\sqrt{\frac{x^2+1}{x^2}}$

$l=\int{\sqrt{\frac{t^2}{t^2-1}}}\frac{dt}{x}$ a a nějak mi uniká jak odstranit to x

Pavel Brožek

↑ marnes:

To $x$ ve jmenovateli si "necháš", dohromady s tím z diferenciálu ti dá $x^2$ , což už se snadno nahradí.

Matematicky to není asi úplně korektní postup (nechávat si tam zároveň x a t), ale dá se ukázat, že to je správně.

$\frac{\sqrt{1+x^2}}{x}\rm{d}x=\frac{t}{x}\frac{t\rm{d}t}{x}=\frac{t^2}{t^2-1}\rm{d}t$

stenly · 21. 01. 2010 21:00

↑ marnes:x^2 ve jmenovateli odmocníš na x a čitatel s odmocninou zvolíš za substituci x^+1=t^2 takže pak ti vyjde ve jmenovateli x^2,což si vyjádříš ze sub.jako x^2=t^2-1!!!

marnes · 21. 01. 2010 21:12

↑ stenly:↑ BrozekP: děkuji moc, už se to začíná rýsovat. Zbytek snad už zvládnu

marnes · 21. 01. 2010 22:04

↑ marnes:Takže vyšlo to, jen pro↑ stenly:, ty meze jsou 2 a 3, jelikož se muselo ještě odmocnit. Ale ještě jednou díky

Matematické Fórum

#1 21. 01. 2010 20:06

délka křivky

#2 21. 01. 2010 20:28

Re: délka křivky

#3 21. 01. 2010 20:33

Re: délka křivky

#4 21. 01. 2010 20:37

Re: délka křivky

#5 21. 01. 2010 20:47

Re: délka křivky

#6 21. 01. 2010 20:57 — Editoval BrozekP (21. 01. 2010 20:58)

Re: délka křivky

#7 21. 01. 2010 21:00

Re: délka křivky

#8 21. 01. 2010 21:12

Re: délka křivky

#9 21. 01. 2010 22:04

Re: délka křivky

Zápatí