Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#9 26. 01. 2010 16:10
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Definiční obory
↑ svizek:
Já jen reaguji na tebou navrhované definiční obory. Vzal jsem hodnotu, která podle tebe do D nepatří, ale funkce tam je přesto definovaná (nebo která podle tebe do D patří, ale funkce tam není definovaná).
Offline
#10 26. 01. 2010 16:16
Re: Definiční obory
↑ halogan:
Nechápu to 3. dosazení. V 10 je funkce definována a 10 patří do 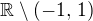 , což napsal kolega. Spíš bych doporučil dosadit nulu…
, což napsal kolega. Spíš bych doporučil dosadit nulu…
Offline
#18 26. 01. 2010 18:45 — Editoval Tychi (26. 01. 2010 19:48)
Re: Definiční obory
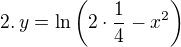
logaritmovat lze pouze čísla větší než nula
což nám dává podmínku 
musíš tedy vyřešit tuto nerovnici a dostat se pokud možno k výsledku, který ti uvedl ↑ zdenek1: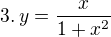
vidíme zlomek, musíme zjistit, jestli se jmenovatel někdy nerovná nula, tyto body je nutné vyřadit z definičního oboru
čili hledáme x taková, že platí 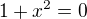
měl bys dojít k tomu, že takové x neexistuje a proto je defininčím oborem celé R.
Vesmír má čas.
Offline


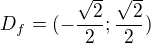

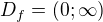
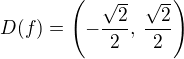 ?
?