Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vázané extrémy funkce 3 proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 01. 2010 02:12
Vázané extrémy funkce 3 proměnných
Zdravím, chtěl bych vás požádat o pomoc s řešením vázaných extrémů
vazby 

Podobně jako u jednodušších variant jsem zkoušel použít Lagrangeovy multiplikátory,
ale nedaří se mi spočítat hodnotu multiplikátorů po dosazení proměnných, vyjádřených z derivací Lagrangeovy funkce,
zpět do vazebních rovnic. Předem díky za reakce
Offline
- (téma jako vyřešené označil(a) M.Hunt)
#2 30. 01. 2010 11:32 — Editoval kaja(z_hajovny) (30. 01. 2010 11:33)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Vázané extrémy funkce 3 proměnných
Zkuste sem tedy dat ten vypocet, at muzeme patrat a pidit se po chybe. Dekuji.
Offline
#4 30. 01. 2010 13:15 — Editoval plisna (30. 01. 2010 13:39)
Re: Vázané extrémy funkce 3 proměnných
↑ M.Hunt: z rovnic 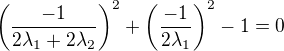 a
a 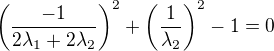 snadno nahledneme, ze musi platit
snadno nahledneme, ze musi platit 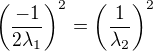 , tedy
, tedy  a po substituci do rovnice
a po substituci do rovnice 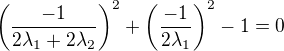 dostavame rovnice pro
dostavame rovnice pro  a
a 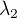 pak jiz snadno dopocteme.
pak jiz snadno dopocteme.
edit: pridano reseni:
Offline
#5 30. 01. 2010 15:39
Re: Vázané extrémy funkce 3 proměnných
Děkuji za ověření a nasměrování správnou cestou, úlohu jsem původně zkoušel řešit podobným způsobem,
ale hodnoty byly v rozporu s výsledky uvedenými u zadání.
Bohužel teprve teď jsem si ověřil, že v zadání uváděné "správné" řešení nesplňuje ani vazební podmínky.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vázané extrémy funkce 3 proměnných (TOTO TÉMA JE VYŘEŠENÉ)

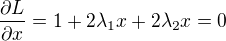







![kopírovat do textarea $[\lambda_1, \lambda_2] = \left[-\frac{\sqrt{2}}{2}, \sqrt{2}\right\]$](/mathtex/64/644d9f03ca8cdd99a36b67aa7ead6aa2.gif)
![kopírovat do textarea $[\lambda_1, \lambda_2] = \left[\frac{\sqrt{2}}{2}, -\sqrt{2}\right\]$](/mathtex/a9/a9d22e2a462b148a48f5cd309bf6c565.gif)
![kopírovat do textarea $[\lambda_1, \lambda_2] = \left[\frac{\sqrt{10}}{6}, \frac{\sqrt{10}}{3}\right\]$](/mathtex/2b/2b5bb821d4180e13f57dc8a9efde8200.gif)
![kopírovat do textarea $[\lambda_1, \lambda_2] = \left[-\frac{\sqrt{10}}{6}, -\frac{\sqrt{10}}{3}\right\]$](/mathtex/2a/2aceb9c87f0c5345528a2ecba622767d.gif)