Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » pocet retazcov (TOTO TÉMA JE VYŘEŠENÉ)
#3 28. 01. 2010 23:49
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: pocet retazcov
↑ exoman: Hledáme počet trojic (A,B,C) podmnožin množiny X takových, že 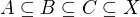 ? Platí |X|=n? V tom případě opravdu není potřeba n půlit, spíše se zamyslet nad tím, do kterých množin může i-tý prvek patřit a využít toho, že takové volby jsou pro všech n prvků nezávislé.
? Platí |X|=n? V tom případě opravdu není potřeba n půlit, spíše se zamyslet nad tím, do kterých množin může i-tý prvek patřit a využít toho, že takové volby jsou pro všech n prvků nezávislé.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 29. 01. 2010 17:59
Re: pocet retazcov
↑ Kondr:
Jen mě napadlo - vzhledem k tomu, že hledáme řetězce dané délky, neměla by být inkluze ostrá? Samozřejmě záleží na definicích, já bych chápal řetězec délky tři jako tříprvkovou lineárně uspořádanou množinu.
Offline
#5 31. 01. 2010 22:54
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: pocet retazcov
↑ Olin: Máš pravdu, smysl to dává s ostrou inkluzí. Svůj příspěvek ale nebudu mazat -- pomocí něj a principu inkluze a exkluze se i správná verze nechá spočítat.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » pocet retazcov (TOTO TÉMA JE VYŘEŠENÉ)
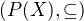 . To by sa malo riesit tym vzorcom s kombinacnym cislom n nad spodnou celou castou n/2?
. To by sa malo riesit tym vzorcom s kombinacnym cislom n nad spodnou celou castou n/2?