Matematické Fórum

Pavel · 26. 01. 2010 14:12 — Editoval Pavel (28. 01. 2010 13:43)

V přechozím příspěvku

http://forum.matweb.cz/viewtopic.php?id=14124

byly zadány rekurentními předpisy dvě posloupnosti a problém byl úspěšně vyřešen. Jak se změní řešení, pokud změníme nerovnost mezi prvními členy těchto posloupností $0<x_1<y_1$ . Jinými slovy

Nechť $\large\color{red}0<y_1<x_1$ a pro každé 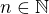$n\in\mathbb{N}$ nechť platí

$\Large x_{n+1}=\frac 12\,(x_n+y_n),\qquad y_{n+1}=\sqrt{x_{n+1}\cdot\, y_n}$

Určete

$\lim_{n\to\infty}x_n$ a $\lim_{n\to\infty}y_n$ .

HINT č.1

Autor skryl část textu. Zobrazit/skrýt!

Marian · 28. 01. 2010 15:03

↑ Pavel:
Ačkoli jsem neměl příliš času na první pokušení o propletených posloupnostech, vůbec bych se nedivil, kdyby se zde vyskytly

Autor skryl část textu. Zobrazit/skrýt!

Pavel · 28. 01. 2010 15:51

↑ Marian:

To je správná cesta. Nedívení se je na místě :-)

check_drummer · 28. 01. 2010 19:50

Pokoušel jsem se různými substitucemi převést úlohu na předchozí případ, ale nezbaralo to. Rovněž neúspěšného bylo hledání funkce s podobnými vlastnostmi jako v případě 1, která ovšem není omezená jako cos. Také nápověda s hyperbolickými funkcemi je pro mě zatím nedostatečná. :-)