Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Zajímavá únorová sumace (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 01. 2010 14:26 — Editoval Marian (29. 01. 2010 14:39)
Zajímavá únorová sumace
Trochu s předstihem jsem zadal únorovou úlohu. Řešit ji ovšem můžete i v lednu ...
Dokažte, že platí
___________
Řešení je tak snadné a hezké, že jsem zatím rozhodnut neposkytovat žádný hint!
Offline
- (téma jako vyřešené označil(a) Marian)
#2 29. 01. 2010 16:59 — Editoval BrozekP (29. 01. 2010 17:02)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zajímavá únorová sumace
Mám asi pouze ošklivé řešení.
Offline
#3 30. 01. 2010 09:33 — Editoval Rumburak (30. 01. 2010 10:09)
Re: Zajímavá únorová sumace
Inspirace mi příšla, když ...
Řešení:
Offline
#4 30. 01. 2010 13:09
Re: Zajímavá únorová sumace
↑ BrozekP:↑ Rumburak:
Zajímavé postřehy. Mám jiné řešení a nedivil bych se, kdyby někdo přišel ještě s jiným nápadem. Nechám ještě čas na rozmyšlenou ostatním (třeba do února :-) ...
Offline
#5 01. 02. 2010 09:39 — Editoval Rumburak (01. 02. 2010 11:01)
#6 01. 02. 2010 22:11
Re: Zajímavá únorová sumace
Představím nyní své řešení, které využívá jistých funkcionálních identit ...
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Zajímavá únorová sumace (TOTO TÉMA JE VYŘEŠENÉ)
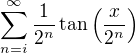
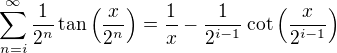 .
. ,
, .
. dostáváme
dostáváme  ,
,  je
je  , z čehož limitou při
, z čehož limitou při  obdržíme
obdržíme 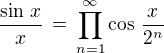 .
. , můžeme rovnost (1) zlogaritmovat na
, můžeme rovnost (1) zlogaritmovat na  , derivací této identity dle x pak získáme
, derivací této identity dle x pak získáme .
. v tom důkazu můžeme zeslabit na
v tom důkazu můžeme zeslabit na  .
. 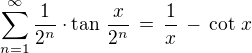
 .
.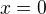 , čímž identita (D) poskytuje zajímavý prostředek k výpočtu ne právě příjemné limity
, čímž identita (D) poskytuje zajímavý prostředek k výpočtu ne právě příjemné limity .
.
 pro uvažovaná x.
pro uvažovaná x. 
 je omezená pro uvažovaná x; přesněji, existuje
je omezená pro uvažovaná x; přesněji, existuje 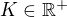 takové, že platí
takové, že platí  . Navíc z konvergence geometrické řady
. Navíc z konvergence geometrické řady  a omezenosti člene
a omezenosti člene  dostáváme odhad
dostáváme odhad
 bylo libovolné.
bylo libovolné.