Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 01. 2010 22:30
Interference a difrakce
Ahoj nevite jak vyresit tento priklad? Dekuji
Světlo ze sodíkové výbojky o vlnové délce λ = 589 nm dopadá pod úhlem α = 30o na optickou mřížku 10 mm širokou. Maximum třetího řádu, které se vytvoří na stínítku vzdáleném 1 m od mřížky, je vzdáleno od maxima nultého řádu 20 mm. Určete celkový počet vrypů na mřížce .
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
- (téma jako vyřešené označil(a) medvidek)
#3 29. 01. 2010 03:02 — Editoval medvidek (01. 02. 2010 04:21)
Re: Interference a difrakce
↑ gekoncik:
Jako správný praktik jsi mohl uvést, zda se jedná o mřížku transmisní nebo reflexní, nebo i nakreslit obrázek :-)
Z mřížkové rovnice  vypočteš mřížkovou konstantu
vypočteš mřížkovou konstantu 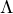 , tj. prostorovou periodu vrypů a převedeš na počet vrypů na 1 cm.
, tj. prostorovou periodu vrypů a převedeš na počet vrypů na 1 cm.
To je všechno.
---------------------------------------------------------------------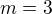 je řád difrakčního maxima,
je řád difrakčního maxima,  je vlnová délka,
je vlnová délka,  je sinus úhlu dopadu,
je sinus úhlu dopadu,
EDIT: až do tohoto místa je můj příspěvek v pořádku.
V následujícím řádku jsou nesprávně použité číselné hodnoty (chyba vznikla z toho, že jsem bral  jako úhel mezi nultým a třetím difrakčním maximem).
jako úhel mezi nultým a třetím difrakčním maximem).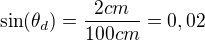 je sinus úhlu difrakčního maxima 3. řádu.
je sinus úhlu difrakčního maxima 3. řádu.
=>  , na délce 1 cm to bude 2716 vrypů.
, na délce 1 cm to bude 2716 vrypů.
Tudíž i výpočet mřížkové konstanty 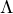 a počtu vrypů je nesprávný :-(
a počtu vrypů je nesprávný :-(
Vysvětlení mřížkové rovnice vč. obrázku a opraveného výpočtu uvedu v následujících příspěvcích.
Offline
#5 29. 01. 2010 20:05
Re: Interference a difrakce
↑ gekoncik: Tady se něco o ohybových jevech a mřížce dozvíš více :
http://www.aldebaran.cz/studium/fyzika/ … p.html#mr1
http://fyzika.jreichl.com/index.php?sek … p;page=461
http://vega.fjfi.cvut.cz/docs/pvok/node120.html
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#6 29. 01. 2010 20:33
Re: Interference a difrakce
↑ medvidek: Dobrý den Ivane :-)
chci se zeptat , proč se lišíme ve výpočtu a ještě takový dotaz možná hloupý , co je přesně to  a co je sinus úhlu difrakčního maxima ( 0,02) s tím jsem v úloze nepočítala , je to velká chyba ?
a co je sinus úhlu difrakčního maxima ( 0,02) s tím jsem v úloze nepočítala , je to velká chyba ?
Děkuji za odpovědiˇ. 
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#7 01. 02. 2010 07:11
Re: Interference a difrakce
Omlouvám se za svou nepozornost při použití mřížkové rovnice v příspěvku #3.
Za trest jsem vytvořil obrázek, na kterém se pokusím všechno vysvětlit :-)
Nyní napíšu mřížkovou rovnici
Úhly 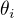 a
a  jsou měřeny od kolmice na mřížku,
jsou měřeny od kolmice na mřížku,  je řád difrakce,
je řád difrakce,  je vlnová délka.
je vlnová délka. 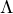 je vzdálenost mezi štěrbinami mřížky (někdy se tomu
je vzdálenost mezi štěrbinami mřížky (někdy se tomu 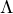 říká mřížková konstanta - nejspíš proto, že reálné mřížky nemusí mít jen štěrbiny a vrypy, ale mohou mít téměř libovolnou periodickou strukturu).
říká mřížková konstanta - nejspíš proto, že reálné mřížky nemusí mít jen štěrbiny a vrypy, ale mohou mít téměř libovolnou periodickou strukturu).
Z mřížkové rovnice můžeme vyjádřit  , což je počet štěrbin na jeden metr mřížky:
, což je počet štěrbin na jeden metr mřížky: 
Difrakcí dojde k ohybu paprsku o úhel  , a ne o úhel
, a ne o úhel  , jak by jsi někdo (např. já :-) mohl myslet.
, jak by jsi někdo (např. já :-) mohl myslet.
Z obrázku je vidět, že 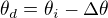 , přičemž
, přičemž 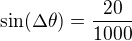
Po dosazení za 
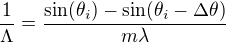
Naše mřížka nemá šířku 1 metr, ale jen 1 cm, takže počet štěrbin  bude 100x menší:
bude 100x menší:
Kdo chce, může sem dosadit a mělo by mu vyjít N=98,588.
Po dalších úpravách lze dostat následující aproximativní vztah
Offline
#8 01. 02. 2010 09:03 — Editoval medvidek (01. 02. 2010 09:05)
Re: Interference a difrakce
↑ Ivana:
Zdravím Ivano :-)
To  není nic jiného než
není nic jiného než 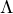 , neboli vzdálenost štěrbin/vrypů v mřížce.
, neboli vzdálenost štěrbin/vrypů v mřížce.
V Reichlově encyklopedii http://fyzika.jreichl.com/index.php?sek … p;page=461 je uveden vztah pro disperzi na mřížce
Tento vztah dostaneme, zvolíme-li v mřížkové rovnici 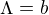 ,
,  (tj. paprsek dopadající kolmo na mřížku),
(tj. paprsek dopadající kolmo na mřížku),  ,
,  .
.
Mřížková rovnice je jen určitým zobecněním tohoto vztahu.
Odvození mřížkové rovnice je principiálně stejně jednoduché. Máte-li někdo zájem, mohu ho sem také uvést.
Offline
#9 01. 02. 2010 19:13 — Editoval Ivana (01. 02. 2010 20:07)
Re: Interference a difrakce
↑ medvidek:Zdravím Ivane :-) , děkuji za odpovědˇ , ještě si řešení potřebuji promyslet . Hezký večer :-) .
PS : Budeš-li mít čas , poprosím o odvození mřížkové rovnice . Ostatnímu výkladu rozumím .
Děkuji :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#10 01. 02. 2010 20:30
Re: Interference a difrakce
↑ medvidek:
A ještě nevím jak upravit 
na tento výraz 
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#11 02. 02. 2010 02:35
Re: Interference a difrakce
↑ Ivana:
Začnu třeba tím, že ukážu úpravu výrazu  .
.
Jmenovatel zůstává stejný, budu tedy zapisovat jen úpravy čitatele: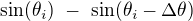

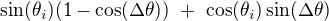
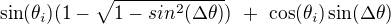
Vzhledem k tomu, že úhel  je poměrně malý - v konkrétním případě
je poměrně malý - v konkrétním případě 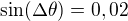 ,
,
bude člen  nevýznamný ve srovnání s
nevýznamný ve srovnání s  .
.
Proto můžeme psát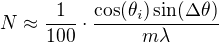
Offline
#12 02. 02. 2010 05:03 — Editoval medvidek (02. 02. 2010 05:04)
Re: Interference a difrakce
↑ Ivana:
Hezký ... (hezkou noc?) , Ivano :-)
Pro odvození mřížkové rovnice použiju obrázek
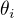 a
a  jsou opět úhly mezi paprskem a kolmicí na mřížku. V obrázku kolmice není zakreslena, ale snad si to každý dokáže představit.
jsou opět úhly mezi paprskem a kolmicí na mřížku. V obrázku kolmice není zakreslena, ale snad si to každý dokáže představit. 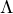 je vzdálenost otvorů v mřížce, zároveň je to společná přepona dvou pravoúhlých trojůhelníků.
je vzdálenost otvorů v mřížce, zároveň je to společná přepona dvou pravoúhlých trojůhelníků.
Z obrázku je patrné, že dráhový rozdíl, který vzniká mezi paprsky procházejícími mřížkou, bude .
.
Aby mohlo vzniknout difrakční maximum, musí paprsky vystupující z mřížky interferovat konstruktivně - to je tzv. podmínka fázového synchronizmu (někdy, zejména u objemových mřížek se tomu říká Braggova podmínka). Tato podmínka je splněna, když je dráhový rozdíl celočíselným násobkem vlnové délky: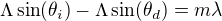
To už je jen jiný tvar mřížkové rovnice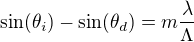
Offline
#13 02. 02. 2010 20:24 — Editoval Ivana (02. 02. 2010 21:38)
Re: Interference a difrakce
↑ medvidek: Zdravím Ivane a moc děkuji :-) . Pořádně si to nastuduji :-)
...o něco později :
Tak tvůj postup jsem prošla , pochopila a posílám své doplněné řešení s celým výpočtem pro N .. počet štěrbin : .jpg)
Ještě jednou děkuji za vysvětlení odvození mřížkové rovnice :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
