Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 02. 2010 15:46
Slovne ulohy - mix
Ahojte,
bojujem s tymito zadaniami, ale dochadzaju mi sily ... Pomoze niekto ?
Prvu som zvladol, vlozim neskor riesenie...
1. Lukáš vyrábal malému bratovi Adamovi šarkana. Vystrihol z papiera veľký pravidelný šesťuholník s obsahom 60 cm štvorcových. Adam sa hneď rozplakal, že on chcel šarkana a nie takého obra. Lukáš mávol rukou, vzal nožnice a z každého rohu kus odstrihol. Vytvoril šesťuholník, ktorého vrcholy boli v stredoch strán pôvodného šarkana. O koľko cm štvrocvých takto zmenšil šarkana?
2. Kukučka v hodinách je zle nastavená a nekuká vtedy, keď trea. Kuká len vtedy, keď ručičky zvierajú uhol 97 stupňov. Hodinky v tomto momente ukazujú 8:00. Kedy najbližšie zakuká kukučka??
3. Rodičom Aprílovcom sa podaril nezvyčajný kúsok - všetkých ich sedem detí má narodeniny v ten istý deň - 1. apríla. Tento rok oslávili 8, 10, 14, 16, 18, 20 a 26 rokov. Hoci majú veľký dom, nemôže mať každý z nich vlastnú izbu. Preto traja spia v spálni na prízemí a štyria v spálni na poschodí. Navyše ocko- matematik - urobil rozdelenie do izieb dosť netradične: obyvatelia spodnej spálne majú rovnaký priemerný vek ako obyvatelia hornej spálne. A to platí dokonca aj vtedy, keď sa najmladší dvaja súrodenci popletú a vymenia si postele. Koľko rokov má každý z obyvateľov spodnej spálne?
4. Michal sa cez prázdniny vybral na bicykli za kamarátom do susednej dediny. Prvú tretinu cesty šiel po rovinke rýchlosťou 24 km/hod, ďalšiu štvrtinu cesty stúpal do kopca rýchlosťou 12 kkm/hod a nakoniec sa už len spustil dolu kopcom rýchlosťou 36 km/hod. Aká bola jeho priemerná rýchlosť?
5. Pred polročnou klasifikáciou učiteľ na hodine vyhlásil: „zajtra budete písať esej. Môžete sa rozhodnúť, či ju budete písať samostatne alebo vo dvojici chlapec+dievča.“ Na druhý deň písalo vo dvojici 2/3 chlapcov a 3/5 dievčat triedy. Aká časť žiakov triedy písala esej samostatne? Výsledok uveď zlomkom v základnom tvare.
Dakujem
Offline
- (téma jako vyřešené označil(a) zdenek1)
#2 04. 02. 2010 16:02
Re: Slovne ulohy - mix
2)
mno představme si, že co minuta, to 360°/60 = 6°. Tedy každou minutu se minutová ručička pohne o 6°.
-> předpokládám, že posun hodinové ručičky můžeme zanedbat..
-> je-li minutová na 0 (12) a hodinová na 8, znamená to, že je mezi nimi 8*5 = 40minut -> 40*6° = 240°. Každou minutu zmenšíme tento úhel o 6°
-> chceme, aby zbylo 97°, rozdíl musí činit 240°-97° = 143° -> 143/6 = 23+5/6 minuty = 23minut a 50 vteřin od počátečního okamžiku (8:00 -> kukat budou v 8:23:50)
Offline
#3 04. 02. 2010 16:12
Re: Slovne ulohy - mix
3) bohužel slovenštině nerozumím natolik, abych pochopil zadání.. jak že tedy mají spát?
4) označme si celkovou dráhu jako "s." Víme tedy:
rovinka... 1/3 * s ... 24 km*hod^(-1)
nahoru... 1/4 * s ... 12 km*hod^(-1)
dolu ...... x*s ... 36 km*hod^(-1)
- musíme si nejprve spočítat, jaká část jeho cesty vedla z kopce:
musí platit: s = s
cestu si můžeme rozložit na jednotlivé úseky: 1/3 * s + 1/4 * s + x*s = s
vytkneme a pokrátíme: 1/3 + 1/4 + x = 1
odtud: x = 1- 1/3 - 1/4 = (12 -4 - 3)/12 = 5/12
nyní máme všechny potřebné údaje, zbývá dopočítat průměrnou rychlost "v_p:"
v_p = 1/3 * 24 + 1/4 * 12 + 5/12 * 36 = 8 + 3 + 15 = 26 km * hod^(-1)
Offline
#5 04. 02. 2010 16:39 — Editoval Doxxik (04. 02. 2010 16:40)
Re: Slovne ulohy - mix
díky ;)
takže 3)
veky dětí: 8, 10, 14, 16, 18, 20, 26
- to, že vzájemná výměna nejmladších svou nemění průměr značí (nebo by mohlo), že jsou na stejném podlaží..
a - průměr 1 (přízemí)
b - průměr 2 (patro)
- musí platit: a = b
- označíme-li si věky písmeny, bude to vypadat nějak takhle:
(m+n+o+p)/4 = (x+y+z)/3
protože nejmladší (pravděp.) spí spolu na patře, aktuální věkový průměr patra je moc malý (9let) -> musíme jej zvýšit (takto nízký z ostatních hodnot nezískáme) -> bude s nimi spát i nejstarší -> věk průměr sice stoupnul, ale pouze na 14,6 - a protože nám zbývají hodnoty jen (kromě jedné) vyšší, je zřejmé, že i tento věk. průměr je příliš nízký -> přidáme dalšího -> nejlépe druhého nejstaršího, aby se průměrný věk více změnil. Zbytek dáme na druhé patro
(26+8+10+20)/4 =(14+18+16)/4
16 = 16
edit: není to moc pěkné řešení.. třeba se najde někdo, kdo bude mít lepší nápad.. (já ale už musím jít..)
zatím ;)
Offline
#6 04. 02. 2010 16:48
Re: Slovne ulohy - mix
1.) moje riesenie sarkana:
Pomocou vzorca na vypocet obsahu 6-uholnika zistim dlzku strany: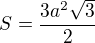
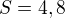
Dalej zistim vysku trjuholnika, co bude zaroven aj dlzka strany noveho 6-uholnika: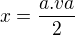
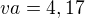
Pomocou prveho vzorca vypocitam obsah noveho 6-uholnika ( = 45 ), a odpocitam ho
od povodneho.
Rozdiel mi vysiel 15 cm2.
Offline