Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 02. 2010 15:14
Re: Ostroúhlý trojúhelník
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 05. 02. 2010 15:23 — Editoval Pavel (05. 02. 2010 15:25)
Re: Ostroúhlý trojúhelník
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 05. 02. 2010 16:02
Re: Ostroúhlý trojúhelník
↑ lukaszh:↑ Pavel:
Oba dva máte podobné úvahy. Pavel nicméně (jak je jeho dobrým zvykem) dokončil zcela.
Znám jiné řešení. Myslím, že je snažší.
Offline
#5 05. 02. 2010 16:45
Re: Ostroúhlý trojúhelník
Jen bych poznamenal, že nerovnost je opravdu "velkorysá", co se týče rozdílu mezi dolním odhadem levé a horním odhadem pravé strany, jelikož
Offline
#6 05. 02. 2010 17:25
Re: Ostroúhlý trojúhelník
↑ Olin:
S touto velkorysostí musím souhlasit. Ovšem na první pohled není tolik jasné, jak to vlastně s nerovností je. Navíc tento velkorysý odhad se může hodit při řešení některých úloh o trojúhelnících.
Offline

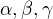 označují vnitřní úhly u vrcholů ostroúhlého trojúhelníku ABC. Dokažte, že platí nerovnost
označují vnitřní úhly u vrcholů ostroúhlého trojúhelníku ABC. Dokažte, že platí nerovnost




 ,
,  a
a  vnitřní úhly ostroúhlého trojúhelníku ABC, pak
vnitřní úhly ostroúhlého trojúhelníku ABC, pak  . Tzn
. Tzn


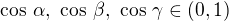 .
. . Tedy
. Tedy  , podobně pro siny ostatních úhlů. Proto
, podobně pro siny ostatních úhlů. Proto
 a
a 
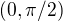 konvexní. Využije se totiž faktu, že platí
konvexní. Využije se totiž faktu, že platí  .
.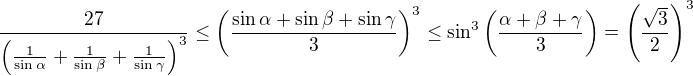 .
.