Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jednotkový vektor kolmý k daným vektorům (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 01. 2010 17:57
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Jednotkový vektor kolmý k daným vektorům
Ahoj, doufám, že poslední dotaz... Mám zadaný úkol: Najděte jednotkový vektor kolmý k vektorům 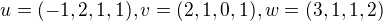 A vůbec si nevím rady. Není to ani ve skriptech. Ani v řešených příkladech ani ve sbírce úloh. Dokonce ani v Olšákovi jsem to nenašel... Mohl by mi někdo poradit? Prosím?
A vůbec si nevím rady. Není to ani ve skriptech. Ani v řešených příkladech ani ve sbírce úloh. Dokonce ani v Olšákovi jsem to nenašel... Mohl by mi někdo poradit? Prosím?
Offline
- (téma jako vyřešené označil(a) ondrej.hav)
#2 11. 01. 2010 18:06
Re: Jednotkový vektor kolmý k daným vektorům
↑ ondrej.hav: ma-li byt vektor  kolmy ke vsem vektorum, musi platit
kolmy ke vsem vektorum, musi platit 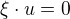 ,
, 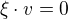 ,
, 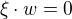 , coz povede na soustavu rovnic pro slozky vektoru
, coz povede na soustavu rovnic pro slozky vektoru 
Offline
#3 11. 01. 2010 18:25 — Editoval ondrej.hav (11. 01. 2010 18:49)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Jednotkový vektor kolmý k daným vektorům
↑ plisna:Jo to mě pak napadlo, akorat nevim jestli ten vektor co z toho vypadne bude jednotkovy... ? nebo to pak ještě mohu nějak dodělat? Vyšlo mi například 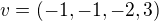
EDIT: Tam bude asi ta norma že? Jsem nějak našel na wiky... Ale stejně nevím jak na to :-(
EDIT: Aha 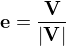 A jestli je velikost vektoru normálně odmocnina z druhých mocnin jednotlivých složek
A jestli je velikost vektoru normálně odmocnina z druhých mocnin jednotlivých složek 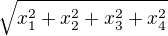 , tak by to mělo být
, tak by to mělo být 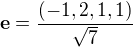 takže ten výslednej jednotkovej vektor by měl být
takže ten výslednej jednotkovej vektor by měl být 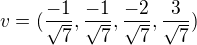 Je to tak?
Je to tak?
EDIT: Chyba... koukal jsem se jinam :-D Mělo by to být 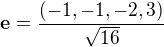 Teď už je to dobře?
Teď už je to dobře?
Offline
#4 11. 01. 2010 18:38
Re: Jednotkový vektor kolmý k daným vektorům
↑ ondrej.hav: ano, pokud chces, aby dany vektor byl jednotkovy, tak jej musis jeste znormovat, tj. spocitat si 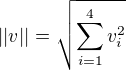 a pak normovany vektor
a pak normovany vektor 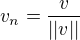
Offline
#6 09. 02. 2010 19:17
Re: Jednotkový vektor kolmý k daným vektorům
↑ johnyQ:
Operácia . v tomto prípade znamená skalárny súčin. To znamená, že ak má byť vektor  kolmý k vektorom u,v,w. potom
kolmý k vektorom u,v,w. potom
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#8 09. 02. 2010 19:26
Re: Jednotkový vektor kolmý k daným vektorům
tak jsem tu soustavu upravil a vyslo mi
-1 2 1 1
0 5 2 3
0 0 6 4
tim se dostavam k problemu jak se dostanu k tomu vektoru, ktery je kolmy na ty tri co jsou v zadani
a pokud jsem pochopil spravne postup tak ten vektor, ktery mi ma zrejme vyjit z te soustavy musim jeste prevest na jednotkovy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jednotkový vektor kolmý k daným vektorům (TOTO TÉMA JE VYŘEŠENÉ)
