Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 02. 2010 11:46 — Editoval Balcik (10. 02. 2010 13:24)
Inverzní funkce
Je dána fce: f:y= sqr(x) +1 / sqr(x) -1
a)Určete D(f),H(f) => D(f)= (1;nekonečno); H(f)= R- {1}
b)Je-li fce prostá - napište inverzní funkci a určete její D(f^-1] a H(f^-1)
inv.funkce: x = sqr(y) +1 / sqr(y) -1
... po úpravách mi vyšlo: y= x^2*y -x^2-1
Je toto správně?
Offline
- (téma jako vyřešené označil(a) Balcik)
#2 10. 02. 2010 12:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inverzní funkce
↑ Balcik:
Zdravím,
nejsem si úpně jistá se zadáním - je to tak? a]  nebo b]
nebo b]  ? Děkuji.
? Děkuji.
v def. oboru D(f) není zohledněna odmocnina (argument sudé odmocniny má být číslo nezáporné), zbytek až po upřesnění zadání.
Offline



 , po prejmenovani
, po prejmenovani  souhlasi? Pokud ano, tak si překontroluj zbytek.
souhlasi? Pokud ano, tak si překontroluj zbytek.

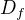 i
i  je špatně.
je špatně.

