Matematické Fórum

Pavel Brožek

Zadání:

Dvě autíčka na dálkové ovládání o hmotnostech $m=2 \textrm{kg}$ jedou vedle sebe stejnou rychlostí o velikosti $v_1=v_2=4 \frac{\textrm{m}}{\textrm{s}}$ . Zatímco první autíčko se pohybuje dál rovnoměrně přímočaře, druhé začne zrychlovat ve směru jízdy a poté, co spotřebuje veškerou zbylou energii ve svých bateriích $E=128 \textrm{J}$ , se bude dál pohybovat rychlostí $v_2'$ . Určete rychlost druhého autíčka $v_2'$ z pohledu stojícího pozorovatele.

(Pozn.: Zanedbáváme veškeré energetické ztráty v důsledku tření, na rovnoměrný přímočarý pohyb tedy autíčko nepotřebuje dodávat energii.)

1. řešení:
Druhé autíčko má na počátku kinetickou energii $E_k=\frac12mv_1^2=\frac12\cdot2\cdot4^2=16\textrm{J}$ . Veškerá dodaná energie se přemění na zvýšení kinetické energie autíčka, na konci tedy bude mít kinetickou energii $E_k'=E_k+E=16+128=144\textrm{J}$ . Jeho konečnou rychlost $v_2'$ tak dostaneme ze vztahu $E_k'=\frac12mv_2'^2$ :

$v_2'=\sqrt{\frac{2E_k'}{m}}=\sqrt{\frac{2\cdot144}{2}}=\sqrt{144}=12\frac{\textrm{m}}{\textrm{s}}$ .

2. řešení:
Z pohledu prvního autíčka druhé autíčko stojí, jeho kinetická energie je tedy $E_k=0\textrm{J}$ . Veškerá dodaná energie se přemění na zvýšení kinetické energie autíčka, na konci tedy bude mít druhé autíčko z pohledu prvního autíčka kinetickou energii $E_k'=E_k+E=0+128=128\textrm{J}$ . Konečnou rychlost druhého autíčka vůči prvnímu autíčku (označme ji $\bar{v_2}'$ ) tak dostaneme ze vztahu $E_k'=\frac12m\bar{v_2}'^2$ :

$\bar{v_2}'=\sqrt{\frac{2E_k'}{m}}=\sqrt{\frac{2\cdot128}{2}}=\sqrt{128}\approx11,3\frac{\textrm{m}}{\textrm{s}}$ .

To musíme převést do soustavy stojícího pozorovatele. Ten tedy uvidí, jak na konci druhé autíčko jede rychlostí $v_2'=\bar{v_2}'+v_1\approx11,3+4=15,3\frac{\textrm{m}}{\textrm{s}}$

Je zřejmé, že se oba výsledky vzájemně vylučují. Který je ale správný? Nebo není správný ani jeden? Proč? :-)

check_drummer · 27. 12. 2009 01:41

↑ BrozekP:

Sice nejsem fyzik a je už pozdě :-), ale

Autor skryl část textu. Zobrazit/skrýt!

FailED · 27. 12. 2009 12:21 — Editoval FailED (27. 12. 2009 12:37)

↑ BrozekP:
Tak jsem taky něco zkusil, snad to není úplně špatně.

Autor skryl část textu. Zobrazit/skrýt!

Pavel Brožek

↑ check_drummer:

Autor skryl část textu. Zobrazit/skrýt!

↑ FailED:

Autor skryl část textu. Zobrazit/skrýt!

Nepozastavujte se prosím nad nesmyslností konkrétních čísel pro autíčko na dálkové ovládání, čísla jsem si vymýšlel. Pokud tedy vyjde rychlost $v_2'=4\cdot10^{8}\ \textrm{ms}^{-1}$ , může to být správně (neříkám, že je :-) ).

check_drummer · 27. 12. 2009 13:54

↑ BrozekP:

Autor skryl část textu. Zobrazit/skrýt!

Pavel Brožek · 27. 12. 2009 14:03

↑ check_drummer:

Autor skryl část textu. Zobrazit/skrýt!

FailED · 27. 12. 2009 14:23

↑ BrozekP:

Autor skryl část textu. Zobrazit/skrýt!

Pavel Brožek

↑ FailED:

Autor skryl část textu. Zobrazit/skrýt!

check_drummer · 28. 12. 2009 15:48

BrozekP napsal(a):
↑ check_drummer:

Autor skryl část textu. Zobrazit/skrýt!
Skrytý text:

Pro baterku, která urychluje druhé autíčko, toto autíčko již nepochybně nějakou energii má.
Když se na autíčko podívá baterka (která je pevně umístěna v autíčku), uvidí nehybné autíčko, proč by tedy mělo mít nějakou enerii?

Speciální teorie relativity není k vyřešení potřeba, vystačíme si s Newtonovou mechanikou :-).

Baterka neuvidí nehybné autíčko, protože se mu točí kolečka. :-)

Ale v podstatě teď stojím na tom, že nevím, co je to energie. :-)) A jaký je vztah mezi energiemi pro různé vztažné soustavy - pakliže má otázka smysl.

Pavel Brožek

↑ check_drummer:

Hmotnost koleček bude nulová (limitně si to snad dokážeme představit) :-)

V této úloze stačí vědět, že kinetická energie tělesa hmotnosti $m$ a rychlosti $v$ je $\frac12mv^2$ (v různých soustavách tedy může být různá) a že existuje i jiná energie než kinetická. Platí zákon zachování energie:

Wikipedie napsal(a):
Celková energie izolované soustavy zůstává konstantní při všech dějích, které v ní probíhají.

V našem případě stačí uvažovat pouze tu kinetickou energii a "energii neznámého typu" v baterii, která je z hlediska všech soustav stejná. Podstatné je, že platí zákon zachování energie.

(Trochu jsem upravil tvůj příspěvek, měl jsi tam špatně tagy a rozhodilo to celou stránku)

medvidek

Jestli tento problém již považujete za vyřešený, budu zde vystupovat v roli hloupého :-).
Na druhé straně nechci nikomu pokazit radost z existující "záhady", proto jen taková myšlenka, popř. inspirace.

Co takhle představit si sebe na klesajícím pohyblivém chodníku jak šlapete stále nahoru, a přitom jste stále na stejném místě. Kam jen ta energie mizí? Nebo si snad někdo myslí, že žádnou práci nekoná? ..., možná by někomu mohlo vadit, že ten chodník je šikmý. Tak si ho srovnejte do vodorovné polohy a začněte zrychlovat (myslím sebe vůči tomu chodníku).

medvidek · 07. 01. 2010 04:21

↑ BrozekP:
Asi by se zde našlo více řešitelů, pokud by se jednalo o dvě rakety pohybující se relativistickými rychlostmi :-)
Ale autíčka?! Hm hm..

lukaszh · 11. 02. 2010 15:07

↑ BrozekP:

Moc sa do toho nerozumiem, ale už by som sa rád dozvedel správnu odpoveď :-) Možno úplný nezmysel, ale to čo je v baterke, je podľa mňa poteciálna (skrytá) energia. Naopak autíčko, ktorému sa zdá, že to druhé stojí má tiež energiu (nie nulovú ako je v riešení) ale poteciálnu 16J. Tak?

Pavel Brožek · 11. 02. 2010 16:16

Omlouvám se, nějak jsem na toto téma zapomněl.

↑ lukaszh:
Moc nerozumím, jak to myslíš. V tom druhém řešení přeci sčítám počáteční kinetickou energii a energii v baterii. Kde by vzalo další energii 16J?

lukaszh · 11. 02. 2010 18:05

↑ BrozekP:

No jo, je to blbosť, spätne keď si to rozmýšľam.

medvidek

Budeme-li tuto úlohu řešit jako izolovaný systém 3 těles (autíčko 1, autíčko 2, silnice), budou řešení konsistentní nezávisle na volbě souřadnicové soustavy. Řešení uvedené v prvním příspěvku jako 2. řešení není správné proto, že soustava 2 těles (autíček), není izolovaná - dochází k výměně energie mezi silnicí a autíčkem 2. Řešení, které je uvedeno jako 1. řešení, sice také nepočítá s třetím tělesem, ale lze ho považovat za správné, protože je limitním případem obecnějšího 3-tělesového řešení pro případ, kdy se hmotnost 3. tělesa - silnice blíží k nekonečnu.

Budu-li mít čas (a bude-li zájem), mohu to sem napsat.

EDIT: Ale možná má BrozekP v rukávu něco hezčí, elegantnější :-)

Pavel Brožek

↑ medvidek:

Snad vás nezklamu, nic elegantnějšího nemám, je to přesně tak, jak píšeš :-).

Výpočty nejsou moc hezké, vyjde se ze zákona zachování hybnosti a energie pro druhé autíčko (index 2) a Zemi (index Z):

$p_2+p_Z=p_2'+p_Z'\nl E_{k2}+E_{kZ}+E=E_{k2}'+E_{kZ}'$

Uvedu pouze rychlost druhého autíčka z pohledu prvního:

$\bar{v_2}'=-v_1+\frac{\frac{m_2}{m_Z}v_2+\sqrt{v_2^2+\frac{2E}{m}$1+\frac{m_2}{m_Z}$}}{1+\frac{m_2}{m_Z}}\approx-v_1+\sqrt{v_2^2+\frac{2E}{m}}$ ,

Toto platí pro libovolnou rychlost prvního autíčka 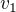$v_1$ , aproximace je pro $m_2\ll m_Z$ . Vidíme tak, že pro $v_1=0\ \rm{ms}^{-1}$ s použitím aproximace skutečně dostáváme 1. řešení.

medvidek

Ještě by mohlo být zajímavé zde popsat, jak bude využita energie baterií 2. autíčka.

Záleží na tom, jakou vztažnou soustavu souřadnic zvolíme pro popis tohoto našeho myšlenkového experimentu.

Pokud řešíme úlohu v soustavě spojené se Zemí (1. řešení), je odpověď intuitivně jasná. Veškerá chemická energie se přemění na zvýšení kinetické energie autíčka.

Pokud se na celou situaci budeme dívat z rovnoměrně se pohybujícího 1. autíčka (2. řešení), dojdeme k jinému závěru.
Vyjdeme ze ZZE, tj. rovnice pro energie z předchozího příspěvku ↑ BrozekP:
$E_{k2}+E_{kZ}+E=E_{k2}'+E_{kZ}'$
Konkrétněji to lze zapsat takto
$0+\frac{1}{2}m_Zv_1^2+E=\frac{1}{2}m_2{\overline{v_2}'}^2+\frac{1}{2}m_Z(v_1+\Delta v_Z)^2$ , kde $\Delta v_Z$ představuje změnu rychlosti Země jako reakci na zrychlování autíčka.
Zároveň platí ZZH:
$p_2+p_Z=p_2'+p_Z'$
Zapsáno konkrétněji
$0+m_Zv_1=-m_2 \overline{v_2}' +m_Z(v_1+\Delta v_Z)$ , neboli $m_2 \overline{v_2}'=m_Z\Delta v_Z$ , tudíž $\Delta v_Z=\frac{m_2}{m_Z}\cdot\overline{v_2}'$
Nyní dosadíme za $\Delta v_Z$ do rovnice pro energie a dále jednoduše upravujeme
$\frac{1}{2}m_Zv_1^2+E=\frac{1}{2}m_2{\overline{v_2}'}^2+\frac{1}{2}m_Z(v_1+\frac{m_2}{m_Z}\cdot\overline{v_2}' )^2$
$E=\frac{1}{2}m_2{\overline{v_2}'}^2+\frac{1}{2}m_Z\left[(v_1+\frac{m_2}{m_Z}\cdot\overline{v_2}' )^2-v_1^2\right]$
$E=\frac{1}{2}m_2{\overline{v_2}'}^2+\frac{1}{2}m_Z\left(2v_1+\frac{m_2}{m_Z}\cdot\overline{v_2}'\right)\frac{m_2}{m_Z}\cdot\overline{v_2}'$
$E=\frac{1}{2}m_2{\overline{v_2}'}^2+\frac{1}{2}\left(2v_1+\frac{m_2}{m_Z}\cdot\overline{v_2}'\right)m_2\overline{v_2}'$
Nyní použijeme aproximaci $m_2\ll m_Z$ a konečně dostaneme
$E \approx \frac{1}{2}m_2{\overline{v_2}'}^2+v_1m_2\overline{v_2}'$
Tento vztah ukazuje, jak se energie baterie $E$ rozdělí na část, která urychlí autíčko 2 a na část, která "zmizí" v silnici (urychlí Zemi).
---------------------------------------------------------------------------------------------------------------------
Uff, tak vidím, že jsem kvůli tomuto vztahu vlastně vypočetl téměř celou úlohu od začátku! Tak už to dotáhnu do konce :-)
---------------------------------------------------------------------------------------------------------------------
Vidíme, že je to kvadratická rovnice s neznámou $\overline{v_2}'$ . Dosadíme číselné hodnoty a vypočteme:
$128=\frac{1}{2}\cdot 2 \cdot {\overline{v_2}'}^2+\ 4 \cdot 2 \cdot \overline{v_2}'={\overline{v_2}'}^2+\ 8{\overline{v_2}'}$ => ${\overline{v_2}'}=8$
Máme tedy výsledek:
Autíčko 2 se bude po spotřebování energie baterie pohybovat vůči autíčku 1 rychlostí 8 m/s.
Z toho plyne, že na zrychlení autíčka bylo využito jen 64 J energie baterie. Zbývajících 64 J se přeneslo do silnice.

Tak takhle to vidí soudruzi sedící v autíčku č.1 :-)