Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 02. 2010 12:25
- princess21
- Příspěvky: 34
- Reputace: 0
exponenciala nerovnica
prosim mohli by ste mi pomoct s tymto prikladom?
4^(x-1) - 17*2^x > -4
nejako s tym neviem pohnut, ta 17 mi to tam vsetko spati :(
Offline
- (téma jako vyřešené označil(a) jelena)
#2 24. 02. 2010 12:44
Re: exponenciala nerovnica
↑ princess21:
Hele, není tam náhodou 4^(x+1)?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 24. 02. 2010 13:10
- princess21
- Příspěvky: 34
- Reputace: 0
Re: exponenciala nerovnica
jezis pardon, ma tam byt x+1... uz sa mi tak zahmlieva pred ocami z tych cisel ze ani nedavam pozor co pisem...
Offline
#4 24. 02. 2010 13:19
Re: exponenciala nerovnica
↑ princess21:
Tak potom
substituce 


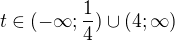 ale vzhledem k podmínce v substituci
ale vzhledem k podmínce v substituci 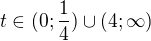
návrat k původní proměnné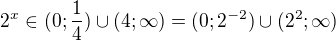

Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 24. 02. 2010 13:32
- princess21
- Příspěvky: 34
- Reputace: 0
Re: exponenciala nerovnica
dakujem pekne za vysvetlenie :)
Offline
