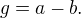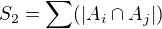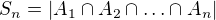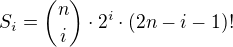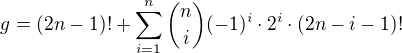Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rozesazení n manželských párů kolem kulatého stolu (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 07. 2009 13:41
Rozesazení n manželských párů kolem kulatého stolu
Nejsem si jist svým postupem výpočtu počtu způsobů, kterými lze rozesadit kolem kulatého stolu n manželských párů tak, aby žádní manželé neseděli vedle sebe:
všech míst kolem stolu je 2n, protože je kulatý, neberu jako další způsob, když sedí stejně, jen pootočeně. Takže prvního z 1. páru dám jedno kam a pro druhého z 1. páru zbývá 2n-3 míst, aby neseděl vedle. Pro 1. z 2. páru zbývá 2n-2 a pro 2. z 2. páru 2n-5 míst, 3. pár obdobně 2n-4 a 2n-7. Protože jevy na sobě závisí, vynásobím to: (2n-3)(2n-2)(2n-5)(2n-4)(2n-7)... a to se rovná (2n-2)!.
Problém je, když většina míst bude obsazená a v případě, že 1. z páru má vlevo i vpravo obsazeno, tak 2. z páru má o 2 větší výběr...
Offline
#2 03. 07. 2009 23:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozesazení n manželských párů kolem kulatého stolu
↑ nordec:
Zdravím,
nevím, jak moje pomoc bude užitečna: zde je název problému na str. 29: http://is.muni.cz/th/14810/prif_r/Kombi … _skole.pdf
pokud zadám vyhledávat "menage problem", tak je to formulováno ještě ve variante "alternace muzu a zen". Tvé zadání je řešeno zde jako "Easier Problem":
http://www.math.utoledo.edu/~dhemmer/4900/menage.pdf
Jedine, co mohu nabidnou, je pomoc s překladem, jinak se ani nesnažím přemyšlet nad řešením, stejně bych nic nevymyslela. Snad někdo z kolegů, děkuji. Ať se to už podaří.
Offline
#3 17. 07. 2009 20:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozesazení n manželských párů kolem kulatého stolu
↑ nordec:
Zdravím,
nedostalo se odpovědí, zda z těch materiálů, co jsem odkazala, se podařilo problém vyřešit, ale mezitím se mi dostalo potěšení konzultovat tuto úlohu s odborníkem, od něhož jsem obdržela i podrobný popis. Tak to zde umístím v původním znění, za které moc a moc děkuji :-)
Zadani:
Mame zjistit, kolika zpusoby muzeme rozesadit kolem kulateho stolu n manzelsky paru tak, aby zadny par nesedel vedle sebe.
Reseni:
Cely problem je mozno resit primo v reci "poctu permutaci" (i kdyz i tam se samozrejme implicitne ci skryte pouziva princip zapojeni a vypojeni), ale ta formulace je dost neohrabana a ja jsem se v tom potom dost ztracel.
Lepsi je resit to v reci mohutnosti (tj. poctu prvku) mnozin vsech permutaci urciteho typu.
Oznacme si A mnozinu vsech moznych rozesazeni 2n osob, tvoricich n manzelskych paru p_1, p_2,..., p_n. Dale si oznacme symbolem A_i, kde i=1, 2, ...,n, mnozinu vsech rozesazeni, ve kterem manzelsky par m_i nesedi vedle sebe.
Jestlize oznacime pocet prvku mnoziny A, tj. |A|, jako a, tedy |A|=a, pocet vsech rozesazeni, kde zadny par nesedi vedle sebe, jako g, a pocet rozesazeni, kde alespon jeden par sedi vedle sede, jako b, potom zjevne, a tedy
Cislo a vyjadruje pocet vsech cyklickych permutaci z 2n prvku, coz je
Potrebujeme tedy vypocitat b.
To ale neni tezke, protoze b je pocet prvku (permutaci), ktere se nachazeji ve sjednoceni vsech mnozin. Oznacme si S_i pocet prvku ve vsech prunicich i ruznych mnozin. Potom
,
dale
pro vsechny dvojice i, j kde i je ruzne od j, (poznámka Jeleny - zřejmě to má být pod znakem SUMA, ale necham to původně - slovně
a tak dale, az
Nyni,
kde to posledni znaminko je + pro n liche a - pro n sude.
Proc to tak delame?
Protoze kdyz spocitame soucet vsech prvku v A_1, A_2, A_3,..., A_n, tak napriklad kazdou permutaci, ktera se nachazi jak v A_1 tak v A_2, jsme zapocitali dvakrat. Proto je musime z toho souctuodecist, cili odecitame
, protoze to je presne ten pocet, ktery byl zapocitan dvakrat. A vsechny tyhle kombinace dvojic mnozin nam daji cislo S_2.
Ale v S_2 jsou zase nektere prvky (permutace) zapocitany vickrat.
Konkretne, prvky zbyly zapocitany v
, dale v
, a konecne v
. Takze to musime zase redukovat. Ale protoze jsme to puvodne odecitali, tak to ted
musime pricist. Da se to lepe videt, kdyz si napiseme:
Ted uz nam jenom zbyva vypocitat S_i pro kazde i = 1, 2,..., n. S_i je soucet prvku ve sjednocenich i-tic mnozin pres vsechny mozne vybery techto i-tic. Takovych i-tic je, tedy pocet kombinaci i-te tridy z n prvku.
Posledni, co musime zjistit, je pocet permutaci v takovem pruniku.
Jelikož vsechny pary jsou rovnocenne, staci, kdyz tento pocet zjistime pro prunik mnozin A_1, A_2,..., A_i, a ve vsech ostatnich toto cislo bude stejne.
Hledame tedy pocet permutaci (rozesazeni), ve kterych pary p_1, p_2,..., p_i sedi vedle sebe, a ostatni libovolne. "Rozesazujeme" tedy 2(n - i) jednotlivcu a i paru, dohromady 2n-i objektu.
To lze ucinit (2n-i-1)! zpusoby, protoze pocet permutaci z (2n - i) prvku, cili (2n - i - 1)! , musime vydelit cislem 2n - i, nebot kazdych 2n - i permutaci je stejnych, lisi se jen cyklickym posunutim okolo stolu, ale nikoliv vzajemnou polohou osob. Protoze jsme vsak kazdy par zatim povazovali za jeden objekt, zbyva vynasobit toto cislo cislem 2^i, nebot kazdy z i paru muze sedet ve dvou ruznych konfiguracich, MZ nebo ZM.
Tedy pocet permutaci v pruniku mnozin A_1, A_2,..., A_i je:a konecne
Nyni vypocteme b jako sumu se stridavymi znamenky a nas vysledek je.
Kolega nordec se pokoušel tento problém řešit také zde: http://forum.matweb.cz/viewtopic.php?id=8743 (snad i s uvedením výsledku) a také bylo rozebráno zde:
http://forum.matweb.cz/viewtopic.php?id=7829
a zde: http://forum.matweb.cz/viewtopic.php?id=9370 a možna i jinde, co jsem nezaznamenala.
------------------------
Doufám, že jsem svou "úpravou" neubližila obsahu příspěvku.
Autorivi řešení velmi a velmi srdečně děkuji a určitě bude odměněn výrobkem (i více výrobky) z kynutého těsta.
Pokud budete mít zájem diskutovat, tak určitě ne se mnou, ale doufám, že autor řešení najde čas, chuť a náladu a diskutovat bude, děkuji :-)
Offline
#4 27. 08. 2009 12:50
Re: Rozesazení n manželských párů kolem kulatého stolu
↑ jelena: Moc děkuji, za tak komplexní rozebrání problému. Byl jsem nějakou dobu pryč, ale rád bych to dořešil:
tedy konečný výsledek, jestli tomu dobře rozumím vyšel 
jenže v http://www.math.utoledo.edu/~dhemmer/4900/menage.pdf uvádějí trochu jiný výsledek: 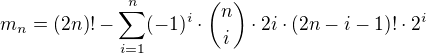

jak je to možné?
Offline
#5 27. 08. 2009 21:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozesazení n manželských párů kolem kulatého stolu
↑ nordec:
Zdravím a děkuji za reakci,
jak jsem psala, není to moje tvorba, s autorem jsem dnes "hovořila" a, jelikož je příliš zaneprazdněn odpočínkem (k čemuž mu přeji dobré pohody), tak autorský komentář zatím nemám, ale mohl by se objevit za nějakou dobu.
Zatím jsem byla upozorněna, že při odvození vzorce pro g nebyl zohledněno ↑ nordec:, že b musí obsahovat (-1)^i, dle závěru zprávy: "Nyni vypocteme b jako sumu se stridavymi znamenky..", tedy ve vzorci oprava: 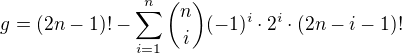
Offline
#6 10. 09. 2009 22:43 — Editoval jelena (10. 09. 2009 22:43)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozesazení n manželských párů kolem kulatého stolu
↑ nordec:
Dostalo se mi dalšího potěšení v podobě slibovaného doplnění k otazce kolegy ↑ nordec:. Autorovi moc děkuji a zde umísťuji odpověď (TeX můj - omluva :-)
...diskutujici kolega ↑ nordec: jenom zapomnel dat do te sumy clen
.
Spravne to je
a tedy vysledek je
a nebo
coz je ale mene "popisne", protoze to zdanlive zacina znamenkem plus.
Ta prvni verze se da cela prepsat do jedne sumy, zacinajici od nuly, a to jako
V tom uvadenem reseni menage.pdf se opravdu resi trosku jiny problem, kde zidle nejsou rovnocenne. To lze videt z toho, ze autor rika napriklad "there are (2n)! ways to seat everyone around the table" coz je pravda, pokud nam zalezi i na tom, na ktere zidli kdo sedi, nejen na vzajemnem rozesazeni. To je videt i v Dukaze, kde se rika "First choose where Dave sits (2n choices)". V nasem pripade se prvni osoba (Dave) posadi kamkoliv, a protoze povazujeme zidle za rovnocenne, tak je to jedinym zpusobem, na rozdil od 2n zpusobu v te druhe verzi problemu.
Konkretně tomuto vysvětlení rozumím, ale že bych kdy dokázala pochopit samostatně něco z tohoto oboru matematiky, to je zcela vyloučeno. Ale podstatné, že rozumím tomuto pokynu: "zvyseny pridel posypky na kolaci :-)" a velký pozdrav autorovi jak odborné časti, tak i pokynu.
------------------------
Přenecham to odbornému publiku k další debatě a pokud se uzná za možné, mohl by se uzavřit i tento dotaz, což sice neřeší problém 8 str. témat bez odpovědí...
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rozesazení n manželských párů kolem kulatého stolu (TOTO TÉMA JE VYŘEŠENÉ)