Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 14. 01. 2010 13:52 — Editoval musixx (14. 01. 2010 13:56)
Re: konstrukce trojúhelníku
Viděl jsem to někde jako "věčný trojúhelník" tohoto fóra. Tady je můj příspěvek:
Ale tohle by určitě spočítal ledaskdo. Ne, že by podle toho (s využitím známých konstrukcí čísel pomocí pravítka, kružítka a nějaké jednotky) nešel onen trojúhelník zkonstruovat, ale není to moc elegantní.
Zkusím se nad tím ještě zamyslet - docela jako výchozí bod si tady tipuju
Taková úloha tady ale přeci nemůže provokovat moc dlouho...
Offline
#3 20. 01. 2010 14:11 — Editoval Wotton (25. 01. 2010 12:34)
Re: konstrukce trojúhelníku
Tak dnes díky kolegyním Tychy a jelena a díky jejich příspěvkům jsem konečně našel způsob jak toto elegantně vyřešit.
1) narýsujem se přímku 
2) narýsujem si kružnici  o poloměru
o poloměru  (kružnice vepsaná) tak aby
(kružnice vepsaná) tak aby  byla její tečna
byla její tečna
3) nechť 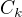 je bod dotyku kružnice
je bod dotyku kružnice  a prímky
a prímky 
4) narýsujem na přímce  bod
bod  tak, že
tak, že 
5) narýsujem přímku  kde
kde  je střed kružnice
je střed kružnice 
6) narýsujem přímky  a
a  rovnoběžné s přímkou
rovnoběžné s přímkou  tak, že vzdálenost přímek
tak, že vzdálenost přímek  a
a  je
je  , a vzdálenost
, a vzdálenost  a
a  je
je  . Přičemž přímka
. Přičemž přímka  leží mezi přímkami
leží mezi přímkami  a
a  . A obě leží na stejné straně přímky
. A obě leží na stejné straně přímky  jako kružnice
jako kružnice 
7) označme  průsečík přímek
průsečík přímek  a
a 
8) spustíme kolmici z bodu  na přímku
na přímku  .
.
9) tam kde tato kolmice protne přímku  je bod
je bod 
Zbytek už je triviální.
Děkuji kolegyním
Dva jsou tisíckrát jeden.
Offline

 je
je  ,
, 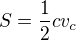 , tedy
, tedy  , tedy
, tedy  , což spolu s
, což spolu s  , a
, a  , což se hodí pro Heronův vzorec v podobě
, což se hodí pro Heronův vzorec v podobě  , což spolu s
, což spolu s  dává možná až překvapivě rychle jediné
dává možná až překvapivě rychle jediné 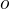 a pomocí již dříve ukázaného
a pomocí již dříve ukázaného  . Zbytek je již snadný.
. Zbytek je již snadný.