Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninový trojúhelník (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 08. 2008 22:58
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Prázdninový trojúhelník
Jak zkonstruovat trojúhelník, je-li zadáno b-a, výška na stranu c a poloměr kružnice vepsané?
Omlouvám se, protože tato úloha tu už jednou byla zadána (je to druhá nejstarší nezodpovězená otázka na tomto fóru). Úloha mi ale přijde tak zajímavá, že stojí za to ji vyřešit. Doufám, že díky tomuto připomenutí a povýšení do stavu prázdninové úlohy se najde někdo, kdo bude vědět jak na ni a nepřibude tak další nezodpovězená otázka :-)
Offline
- (téma jako vyřešené označil(a) Kondr)
#2 28. 08. 2008 23:08
Re: Prázdninový trojúhelník
↑ BrozekP:
Uz jsem si na ni dvakrát našel čas, ale ani jednou jsem se nedopátral rozumné varianty řešení. Hlodá mi dodnes v hlavě. Velice mě těší tvá iniciativa a vzorný zájem o matematiku. Pevně věřím, že se nám podaří na sklonku prázdnin vyřešit pravděpodobně poslední prázdninovou úlohu.
Offline
#3 28. 08. 2008 23:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový trojúhelník
↑ Marian:
Ještě tu je jedna prázdninová úloha, která nebyla uspokojivě vyřešena (trochu zapadla) - Prázdninová diferenciální rovnice. Nedoporučuji nechávat si spočítat výsledek programem (bohužel jsem to udělal), je celkem hezký a pak to svádí hledat metody jak se dostat k tomu výsledku.
Nad trojúhelníkem už jsem nějaký nemalý čas strávil, ale nic mě nenapadlo. Přitom je zřejmé, že řešení se dá spočítat (nevím teda jak analyticky, dostal jsem se pouze ke složitým rovnicím).
Offline
#4 29. 08. 2008 21:15
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový trojúhelník
Při procházení internetu ve snaze najít nějaké konstrukce trojúhelníků, které by mi pomohly vyřešit ten "neřešitelný" trojúhelník, jsem našel jiné zajímavé zadání (asi lehčí, ale nemůžu moc posuzovat, když neznám řešení tohoto trojúhelníku). Zadání bylo i s řešením, takže to tu nezůstane nevyřešené (doufám ale, že tohle už někdo vyřeší :-):
Zkonstruujte trojúhelník, je-li dán jeho obvod, výška na stranu a a úhel alfa.
Offline
#5 30. 08. 2008 00:23 — Editoval Marian (30. 08. 2008 07:19)
Re: Prázdninový trojúhelník
Musel jsem trochu hledat v paměti, jaká je taktika konstrukce trojúhelníků u nichž je zadán obvod a nakonec se podařilo nalézt řešení. Řeším následující úlohu:
Zkonstruujte trojúhelník ABC, je-li dán jeho obvod a+b+c, výška na stranu a a úhel alfa.
Postup konstrukce provedu formou diskuze.
1. Předpokládejme, že takový trojúhelník ABC existuje.
2. Prodloužíme úsečku BC na přímku p procházející body B a C.
3. Na polopřímce CB zkostruujeme bod M takový, že platí |AB|=|BM|.
4. Na polopřímce opačné k polopřímce CB zkonstruujeme bod N takový, že platí |AC|=|CN|.
5. Tudíž je |MN|=a+b+c.
6. Konstruujeme pomocný trojúhelník AMN.
7. V tomto bodě prodiskutuji úhly (všechny budou konvexní), jejichž velikost budu označovat např. |ABC| jako velikost konvexního úhlu u vrcholu B, etc. Platí jistě |ABM|=|BAC|+|ACB|. Protože trojúhelník ABM je rovnoramenný, musí platit |AMB|=|BAM|=1/2*|ABC|. Podobně také platí |CAN|=|ANC|=1/2*|ACB|. Protože platí identita |ABC|+|BCA|+|BAC|=Pi, je 1/2*|ABC|+1/2*|BCA|=Pi/2-1/2*|BAC|. Dále z faktu, že |MAN|=|BAC|+1/2*|ABC|+1/2*|BCA|, máme |MAN|=Pi/2+1/2*|BAC|.
8. Tedy převedli jsme danou úlohu na úlohu konstrukce trojúhelníku AMN s daným úhlem velikosti |MAN|, danou výškou v_a (jež se rovná dané výšce v_a hledaného trojúhelníku ABC) a danou délkou strany a'=|MN|=a+b+c. To se dá ale zkonstruovat pomocí geometrického místa bodů dané vlastnosti - konstrukce je známa.
Offline
#6 30. 08. 2008 01:43
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový trojúhelník
↑ Marian:
Souhlasím s postupem. Jen bych měl pár drobných poznámek:
- v bodě 3 a 4 je to asi prohozené - v bodě 3 by mělo být na polopřímce opačné k polopřímce BC a v bodě 4 zase na polopřímce opačné k polopřímce CB (kvůli jednoznačnosti je to lepší než říct na polopřímce BC - co kdyby |BC|>|AC|)
- součet velikostí vnitřních úhlů v trojúhelníku je Pi
Jinak tam, odkud zadání mám (http://www.staff.ul.ie/acarty/Complete.pdf) je to řešené jinak (konstrukce by asi byla trochu složitější než ta tvoje):
1. Sestrojíme úhel XAY=alfa, přičemž 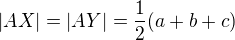 .
.
2. Sestrojíme kolmici p k přímce AX v bodě X a kolmici q k přímce AY v bodě Y, průsečík přímek p a q označíme Z.
3. Sestrojíme kružnici k se středem v bodě Z o poloměru |ZX|=|ZY|.
4. Sestrojíme kružnici l se středem v bodě A o poloměru  (výšky na stranu a)
(výšky na stranu a)
5. Sestrojíme vnitřní společnou tečnu t kružnic k, l.
6. Průsečík přímky t a AX označíme B, průsečík přímky t a AY označíme C. Máme tak trojúhelník ABC.
Offline
#7 30. 08. 2008 07:16 — Editoval Marian (30. 08. 2008 07:16)
Re: Prázdninový trojúhelník
↑ BrozekP:
Už jsem to prohodil. Ten odkaz výše na PDF mi nefunguje. Našel jsem také zajímavou konstrukční úlohu. Pokud někdo chce, může zkusit řešit. Později přidám řešení, které znám já.
Úloha. Sestrojte trojúhelník ABC, je-li dán úhel  , poloměr
, poloměr  kružnice opsané a poloměr
kružnice opsané a poloměr  kružnice vepsané.
kružnice vepsané.
Offline
#8 30. 08. 2008 10:00 — Editoval BrozekP (30. 08. 2008 10:18)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový trojúhelník
↑ Marian:
Bohužel odkaz už mi také nefunguje (včera ale jistě fungoval). Protože ale nefunguje ani http://www.ul.ie (University of Limerick), mohl by to být pouze dočasný výpadek. Verzi v html má google uloženou v cache, nejsou tam ale obrázky:
http://209.85.135.104/search?q=cache:CK … k&cd=1 (je to úloha "triangles 4" na straně 3)
Řešení tvého zadání jsem někde včera viděl, takže bych to prozatím ponechal pro ostatní nevyřešené.
Offline
#9 30. 08. 2008 12:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prázdninový trojúhelník
Zdravím vás :-)
k nevyřešené úloze jsem se také občas vrátila, už jsem zkoušela projit i vlastnosti významných bodů a různé vztahy pro významné přímky trojuhelníku, nebo vztahy postavené na různých způsobéch vyjádření obsahu a také bez výsledku...
Možná pomůže pomůcka z Poláka nebo z Planimetrie pro gymnázia - kde se doporučuje "pokud je zadán součet nebo rozdíl stran, je vhodné využit osovou souměrnost". Uloha, kterou už vyřešil Marian, je v Planimetrii v trochu jiné upravě (obvod a 2 úhly alfa, beta) - ale je to stejná "určitost" úlohy". Teď už podobná zadání řeším slušně, ale, když jsem tuto úlohu viděla před nějakou dobou poprvě, bez řešení, jen s nápovědou, tak jsem pokreslila dost papírů.
Naše nevyřešená úloha se mi zdá být "nedostatečně určitá".
Obrovské množství úloh a řešení je na ruské str., na kterou se odkazoval i Marian http://www.math.ru/lib/cat/geom?n=20&am … _by=author ale, když tam něco hledám, tak se zaseknu na první historické knižce.... a beznádějný případ jsem :-) Takto kolegovi BrozekP naznačuji, že základy ruštiny jsou docela vhodné :-)
Hodně zdaru :-)
Offline
#11 30. 08. 2008 20:50
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový trojúhelník
↑ Ivana:
Bohužel, toto není správné řešení - trojúhelník máš sestrojený pouze pomocí úhlu a poloměru kružnice vepsané. Kružnici opsanou tam sestrojíš až když je trojúhelník hotový. Pokud to takto vše sestrojíš, tak kružnice opsaná bude mít obecně jiný poloměr, než je zadaný. Ty jsi vyřešila úlohu, kdy je místo poloměru kružnice opsané zadaný úhel alfa=90°.
Offline
#12 31. 08. 2008 13:29
Re: Prázdninový trojúhelník
↑ BrozekP:
:-(
Tak budu přemýšlet dál . :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#14 31. 08. 2008 14:20 — Editoval Jorica (31. 08. 2008 14:36)
Re: Prázdninový trojúhelník
↑ radulala:
Zaloz nove tema (prip. 2 temata), protoze ulohy o pohybu a smesich nemaji nic spolecneho s konstrukci trojuhelnika (kam jsi svuj dotaz vlozil(a) nyni) a malokdo by zde neco takoveho hledal. Poloz otazku konkretneji. Uved treba priklad, o ktery jde, jak jsi postupoval(a), prip. co neni jasne.
Pokud ti jde o reseni uloh na smesi obecne, zkus si procist prispevek kolegyne Jeleny prispevek c. 38.
Offline
#16 18. 09. 2008 23:31 — Editoval jelena (18. 09. 2008 23:58)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prázdninový trojúhelník
Zdravím vás :-)
Narazila jsem na zadaní, kde je rozdíl stran (b-a) a kruznice opsana a vepsaná: http://www.studentmatematiky.own.cz/planimetrie.pdf ale je to nad možnost mé představivosti.
Odkaz je na webu kolegy martanko.
Offline
#17 14. 01. 2010 22:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prázdninový trojúhelník
Pozitivní zprávy :-) kolega musixx má návrh na řešení a kolega Wotton je odhodlán problém řešit.
-----
Надежды маленький оркестрик...
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninový trojúhelník (TOTO TÉMA JE VYŘEŠENÉ)

 jsem sestrojila hned a ten třetí
jsem sestrojila hned a ten třetí 
