Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 08. 2010 13:51
Nerovnosti
Dobré odpoledne,
rád bych založil toto téma, kde bych dával nerovnosti,
s kterýma mám problém.
A hned první je:
Dokažte, že pro 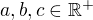
platí 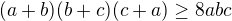 .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
- (téma jako vyřešené označil(a) byk7)
#3 04. 08. 2010 14:18
Re: Nerovnosti
No, pročítám si letošní seriál z PraSátka a tam přesně stojí:
Cvičení. Pro kladná čísla 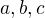 ukažte
ukažte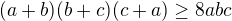
a rozhodněte, zda nerovnost platí i pro reálná čísla.
Návod. Vynásobte tři platné nerovnosti.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#4 04. 08. 2010 15:13 — Editoval Mr.Pinker (04. 08. 2010 15:44)
Re: Nerovnosti
když to budeš postupně upravovat tak ti výjde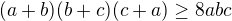
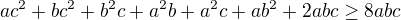
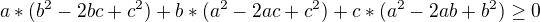
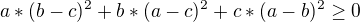
a pokud a b c sou kladná čísla tak součin bude složen jen z kladnejch čísel tudíž zákonitě větší roven nule
je to srozumitelný ?
edit: jo jistě promin to je že dělám kolem x dalších věcí a pak to není pečlivý :-D
Offline
#6 04. 08. 2010 15:35 — Editoval byk7 (04. 08. 2010 15:44)
Re: Nerovnosti
↑ Stýv: v tomhle AG nerovnost jaksi nevidím
Edit: ↑ Mr.Pinker: je to srozumitelné, asi překlep 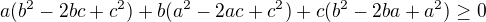
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 04. 08. 2010 15:44
Re: Nerovnosti
↑ petrkovar: ↑ Stýv: stále nic
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#13 17. 08. 2010 17:09
Re: Nerovnosti
↑ byk7: napadl mě jeden důkaz, chtěl bych poprosit o kontrolu:
substituce 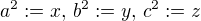 , tedy
, tedy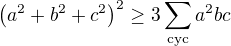 ,
,
po úpravě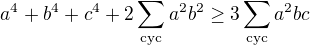 ,
,
ta vznikne součtem tří nerovností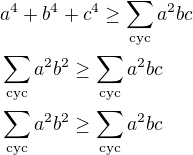 .
.
O platnosti každé z nich se dá přesvědčit pomocí vážené AG nerovnosti.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#15 17. 08. 2010 20:09
Re: Nerovnosti
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline

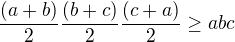 ?
?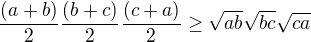 už?
už?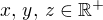 dokažte
dokažte 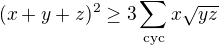 .
.