Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Reciproká vs. Trinomická rovnice + bonus (TOTO TÉMA JE VYŘEŠENÉ)
#28 31. 08. 2010 23:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reciproká vs. Trinomická rovnice + bonus
↑ avalagne:
ano, to už zvladneme. Potom se vratíme k substituci a dopočteme x. Také nezapomeneme, že jeden kořen byl x=1.
Výsledek překontrolujeme zde.
V pořádku?
Offline
#30 01. 09. 2010 00:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reciproká vs. Trinomická rovnice + bonus
Můžeme i D bez "c", ale: převedeme na součinový tvar
převedeme na součinový tvar odsud kořeny y_1=... y_2=
odsud kořeny y_1=... y_2=
Začátek řešení reciproké rovnice byl postaven na tom, že rovnice II. druhu má vždy jeden kořen x=1. Proto jsme mohli dělit (x-1).
Který jste obor, alespoň úplně orientačně. Děkuji.
Offline
#32 01. 09. 2010 00:26 — Editoval jelena (01. 09. 2010 00:28)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reciproká vs. Trinomická rovnice + bonus
↑ avalagne:
Děkuji, tady se také plave. Já se zajimám o zpěv :-)
z toho Wolframu jsou již x.
odsud máme y:  ,
, 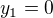 ,
,  , x dopočteme ze substituce.
, x dopočteme ze substituce.
Offline
#33 01. 09. 2010 00:29 — Editoval avalagne (01. 09. 2010 00:39)
Re: Reciproká vs. Trinomická rovnice + bonus
↑ jelena:
Tak co se týče sportu, tak posilovna, jinak nic :D
Jdu to dopočítat zase... Dělám tady ze sebe ****** akorát :))) Ale co už, reciproké rovnice mi opravdu nic neříkali... Teď už aspoň něco vím.
EDIT: Takže teď už opravdu jen dosadit y_1, y_2 do těch substitucí ano?
Offline
#34 01. 09. 2010 00:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reciproká vs. Trinomická rovnice + bonus
↑ avalagne:
Ano, dosadit sem místo y 
No raděj nekomentuj své výkony, ještě se zajimám o čistotu češtiny.
Pro trinomickou rovnici si, prosím, založ nové téma a pro algebru také - s odkazem na kolegu Jarrro.
Ať se vede.
Offline
#35 01. 09. 2010 00:42 — Editoval avalagne (01. 09. 2010 00:47)
Re: Reciproká vs. Trinomická rovnice + bonus
Nadávka nebyla myšlena na nikoho... Už tam není...
Tak už mi vyšlo x^2 + 1 = 0 ... => x_1 = 0 a x_2 = -1...
A druhá 3x^2 + 10x + 3 = 0 ... Takto je to prosím správně? => těch x_1 = -3 a x_2 = -1/3 z Wolframu
Vím, že tě otravuju... S trinomickou větou si hlavu teď dělat nebudu.
Offline
#37 01. 09. 2010 00:52 — Editoval avalagne (01. 09. 2010 09:02)
Re: Reciproká vs. Trinomická rovnice + bonus
↑ jelena:
No protože to je v komplexních číslech? Druhá mocnina je -1
To druhé tedy mám...
EDIT: Nevim proč píšu druhá mocnina, když tam taková není... Je tam první a to je "i"... Takže odpověď je, že kořeny jsou x_1 = i a x_2 = -i v oboru komplexních čísel...
Offline
#38 01. 09. 2010 00:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reciproká vs. Trinomická rovnice + bonus
↑ avalagne:
Ano, tak nějak. Pokud máme 5 kořenů ve shodě s Wolframem, tak bych navrhovala problém "reciproká rovnice" považovat za vyřešený.
Offline
#39 01. 09. 2010 01:01 — Editoval avalagne (01. 09. 2010 01:03)
Re: Reciproká vs. Trinomická rovnice + bonus
↑ jelena:
Uff, je tomu tak... Moc děkuju za snahu a hlavně pevný nervy, který asi hodně pracovali :)
Reciprokou rovnici jsem opravdu viděl a řešil poprvé...
Dávám za vyřešené... Jen nevim, jestli chci vůbec umět trinomickou rovnici, když vidim tohle :D
Offline
#40 01. 09. 2010 01:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reciproká vs. Trinomická rovnice + bonus
Nevim proč píštu druhá mocnina...
v pořádku - tato rovnice  (nebo po přepisu
(nebo po přepisu  ) skutečně říká, že druhá mocnina nějakého čísla je (-1) a to "nějaké" číslo může být i nebo (-i).
) skutečně říká, že druhá mocnina nějakého čísla je (-1) a to "nějaké" číslo může být i nebo (-i).
------------------------------
Ne, jsem absolutně v klidu, neb tu relaxuji.
Trinomická se také podaří.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Reciproká vs. Trinomická rovnice + bonus (TOTO TÉMA JE VYŘEŠENÉ)

 , odsud
, odsud 
 je to jasne proc?
je to jasne proc?  to je v pořádku, kvadratická rovnice.
to je v pořádku, kvadratická rovnice.