Matematické Fórum

Joerex · 23. 10. 2010 19:41

Zde mám několik funkcí kdeje potřeba určit rovnici tečny a normály(2,3,4).Jsou u toho i výsledky,ale nevim postup výpočtu.

http://yfrog.com/n3img1118sj

Stačí tedy naznačit,či rozepsat postup a výpočet již zkusím sám.Díky za rady.

jelena · 23. 10. 2010 21:33

↑ Joerex:

Zdravím, sice ani jednu funkci jsem v odkazu nerozluštila - nečitelné, otočeno atd. ale určitě pomůže tento odkaz, tedy u všech funkcí najdeš derivaci v zadaném bodě a použiješ vzorec pro tečnu a normálu.

V úvodním tématu sekce VŠ jsou online nástroje pro kontrolu. Případně se ozví.

Prosba - označ svá předchozí témata za vyřešená, pokud tomu tak je. Děkuji.

GudMen · 23. 10. 2010 21:56

Podívejme se na třetí příklad.

Protože tečna má být kolmá na přímku $2x-6y+1=0$ , potřebujeme zjistit směrnici normály dané přímky, čímž získáme směrnici hledané tečny $k_t$ . Upravíme tedy přímku do směrnicového tvaru $y=k_p*x+q \rightarrow y=\frac{1}{3}x+\frac{1}{6}$ a získáme směrnici dané přímky $k_p=\frac{1}{3}$ a tu následně převedeme na směrnici normály $k_n=\frac{-1}{k_p} \rightarrow k_n=-3$ . Směrnice hledané tečny tedy je $k_t=-3$ .

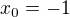Nyní zderivujeme zadanou funkci $f'(x)=[x^3+3x^2-5]'=3x^2+6x$ . První derivace funkce představuje směrnici tečny, a tak platí i následující rovnost $k_t=-3=3x^2+6x$ . Rovnici vyřešíme a dostáváme $x_0=-1$ . Dosadíme $x_0$ do původní rovnice $y_0=x_0^3+3x_0^2-5$ a dostáváme $y_0=-3$ .

Tečný bod $T[x_0,y_0] = T[-1,-3]$ dosadíme do rovnice tečny $(y-y_0)=k_t*(x-x_0)$ a dostáváme požadovaný výsledek $y=-3x-6$ .

Čtvrtý příklad budeš počítat obdobně, akorát v první části získanou směrnici přímky nebudeš převádět na směrnici normály, protože hledáš tečnu rovnoběžnou s danou přímkou, nikoliv kolmou jako v příkladě předchozím. Směrnice normály a směrnice přímky jsou na sebe navzájem kolmé. Bude tedy platit $k_t=k_p$ .

U druhého příkladu již máš určenou první souřadnici tečného bodu $x_0$ , takže stačí dopočítat $y_0$ a dosadit do rovnice tečny (viz. výše) a do rovnice normály $(y-y_0)=k_n*(x-x_0)$

↑ jelena:

Obrázek lze otáčet. ;)

jelena · 23. 10. 2010 22:28

GudMen napsal(a):
↑ jelena:

Obrázek lze otáčet. ;)

:-) děkuji. Dosud jsem na tuto technickou výmoženost nepřišla, vzdy upadám do spánku, když prohlížím takto natočené obrázky, proto se věnují ruční umělecké tvorbě kolegů (to je společná tvorba).

Pokud by kolega použil okno Hledat, tak by našel minimálně toto nebo tamto + místní pravidla ohledně počtu problémů v jednom tématu, označení za vyřešené atd.

--------------------
Zcela vážně: děkuji za přehledné a podrobné řešení.

Joerex · 24. 10. 2010 20:12 — Editoval Joerex (24. 10. 2010 20:14)

↑ GudMen:

Jak mám prosímtě dosadit f(x)=xlnx do toho směrnicového tvaru?(4tý příklad).

jelena · 24. 10. 2010 20:23

↑ Joerex:

do směrnicového tvaru přímky (který konkrétně zápis máš na mysli?) nedosazuje zápis funkce, ale hodnotu funkce f(x_0)=y_0 v bodě x_0, případě hodnotu derivace funkce ve stejném bodě.

Můžeš prosím upřesnit, kam jsi došel v zadání 4). Děkuji.

Joerex · 24. 10. 2010 20:45

↑ jelena:

popravdě moc daleko ne,spočítal jsem derivaci, která mi vyšla ln(x) + 1
potom jsem koukal do odkazu od tebe http://forum.matweb.cz/viewtopic.php?id=401 ,ale pořád nevím ja s tím naložit

jinak zápis funkce,který jsem myslel je y=kp*x + q

GudMen · 24. 10. 2010 20:58

↑ Joerex:

Na směrnicový tvar upravuješ zadanou přímku $2x-2y+3=0$ , ne funkci. Získanou směrnici už nepřevádíš na normálu jako ve třetím příkladě, ale rovnou dosazuješ do rovnice s první derivací funkce.

jelena · 24. 10. 2010 21:03 — Editoval jelena (24. 10. 2010 21:05)

s touto přímkou $2x-2y+3=0$ má být normala rovnoběžná. rovnice normály je $(y-y_0)=-\frac{1}{f^{\prime}(x_0)}(x-x_0)$

upravím si rovnici normály tak, abych viděla stejný normálový vektor, jako u zadané přímky $-\boxed{\frac{1}{f^{\prime}(x_0)}}(x-x_0)+\boxed{-1}y+y_0=0$

a zadanou přímku vydělím 2 $\boxed{1}x{-1}y+3/2=0$ teď mohu "okopírovat" "normalový vektor" jedné a druhé přímky:

$-\boxed{\frac{1}{f^{\prime}(x_0)}}=\boxed{1}$ , místo $f^{\prime}(x_0)$ dosad zápis derivace $\ln(x)+1$ a vypočti x z rovnice, což bude x_0.

Z náhledu již vídím odpověď kolegy GudMen, ale už to tak necham, nebudu mazat (pokud kolega uzná za nevhodné, tak samozřejmě smažu). Děkuji.

Joerex · 24. 10. 2010 21:24

↑ jelena:
x_0 mi vyšlo 1/e^2 ...na zbytek se kouknu zítra abych si v tom udělal pořádek a porozuměl tomu,teď už mi to opravdu nemyslí.Díky za snahu mi pomoci,zítra napíšu jak jsem pokročil.

jelena · 24. 10. 2010 21:51

↑ Joerex:

není za co - vysvětlení poskytl kolega ↑ GudMen: a ve výsledku se shoduješ s výsledkem kolegy Kondra z roku 2007, kolegům děkuji.

Aby se obrázek nemusel otáčet. ...

Matematické Fórum

#1 23. 10. 2010 19:41

Rovnice tečny a normály

#2 23. 10. 2010 21:33

Re: Rovnice tečny a normály

#3 23. 10. 2010 21:56

Re: Rovnice tečny a normály

#4 23. 10. 2010 22:28

Re: Rovnice tečny a normály

GudMen napsal(a):

#5 24. 10. 2010 20:12 — Editoval Joerex (24. 10. 2010 20:14)

Re: Rovnice tečny a normály

#6 24. 10. 2010 20:23

Re: Rovnice tečny a normály

#7 24. 10. 2010 20:45

Re: Rovnice tečny a normály

#8 24. 10. 2010 20:58

Re: Rovnice tečny a normály

#9 24. 10. 2010 21:03 — Editoval jelena (24. 10. 2010 21:05)

Re: Rovnice tečny a normály

#10 24. 10. 2010 21:24

Re: Rovnice tečny a normály

#11 24. 10. 2010 21:51

Re: Rovnice tečny a normály

Zápatí