Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 05. 2011 16:02
určení těžiště
kolegové a kolegyně mohli by jste me prosím nakopnout co s tím mám dělat. Pořád čtu skrypta tam a zpátky a nevím kudy kam
Moc by mi pomohlo kdybyste mi vysvětlili polopatě jak na to
Děkuji
Offline
- (téma jako vyřešené označil(a) jelena)
#4 28. 05. 2011 20:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: určení těžiště
Zdravím,
↑ zdenek1: děkuji.
↑ osshek:
asi těžko někdo chápe, co bys chtěl vysvětlit - nascanuj sem své skrIptum, vyznač řádek, který není jasný, někdo z kolegů snad bude tak hodný a ten konkrétní řádek vysvětli.
Už jsem vysvětlovala ohledně umístění čárek a teček do vět? Posledně jsme Tobě vysvětlovali celým týmem inverzní funkci a dosud nevíme, jaký to mělo efekt. Chybí nám potom evaluace a nemůžeme se zdokonalovat v polopatických výkladech.
------------------------------------
Tedy „jo, přečetl jsem si to skriptum“ (c)
Offline
#5 28. 05. 2011 20:43
Re: určení těžiště
↑ osshek:
Mně osobně třeba tyhle vzorečky docela hezky připomínají vážený průměr. Hlavně u toho pro 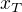 je to podle mého hezky vidět. Rozřežu si to na svislé sloupečky, ty si očísluju, a snažím se najít průměrnou hodnotu z těch čísel, přičemž čím je sloupeček vyšší, tím má větší váhu.
je to podle mého hezky vidět. Rozřežu si to na svislé sloupečky, ty si očísluju, a snažím se najít průměrnou hodnotu z těch čísel, přičemž čím je sloupeček vyšší, tím má větší váhu.
Ale jelena má pravdu, že bys mohl být konkrétnější.
Offline
#6 28. 05. 2011 21:59
#7 28. 05. 2011 22:04
Re: určení těžiště
↑ zdenek1:
Ano, já jsem si toho vědom :-) Proto jsem to taky napsal. Jen jsem byl trochu opatrný, protože by to určitě šlo zdůvodnit i jinak, proč to vypadá zrovna takhle.
Offline
#8 29. 05. 2011 11:18
Re: určení těžiště
kolegové, snažíte se pěkně. to vím že elemety Dx a Dy jsou male derivované částečky a hledám tu která je nejvíce u středu tělesa.
Ale, ce vzorci je : xy*dx/y*dx mě pořád není jasné co mám dosadit místo toho xy a dy/ y * dx. v zadání mám k=4m^2 y(x) =sqrt[3]{kx} co stou funkcí mám udělat a jak ji použít tohle to potřebuji pochopit.
xy*dx/y*dx mě pořád není jasné co mám dosadit místo toho xy a dy/ y * dx. v zadání mám k=4m^2 y(x) =sqrt[3]{kx} co stou funkcí mám udělat a jak ji použít tohle to potřebuji pochopit.
A pro Jelenu, moc děkuji za inverzní funkci dostala jsi 2 ze seminárky.
Děkuji
Offline
#9 29. 05. 2011 11:23 — Editoval LukasM (29. 05. 2011 11:26)
Re: určení těžiště
↑ osshek:
My se snažíme, to ano, ale snažíš se taky ty?
Za prvé myslím, že bys všem ušetřil čas, kdybys rovnou napsal že jenom neumíš spočítat jednoduchý integrál.
Za druhé jak to spočítat ti poslal ↑ zdenek1: hned v první odpovědi, tak si to zkus místo ptaní přečíst.
Edit: Teď jsem si ještě prošel všechna tvoje témata, a opravdu máš nějaký problém s vlastní snahou a pravidly, tak na tom zkus zapracovat.
Offline
#10 29. 05. 2011 13:20
Re: určení těžiště
↑ LukasM: vlastní snaha byla, a když nevím tak se obracím, určitý integral umím. Mě zajímá tohle to 
A ještě něco Lukasi a není jen u tebe, Pozoruji to skoro u všech s akademickým diplomem. Při prosbě o pomoc začnou kopat kolem sebe že mam malo vlatní snahy a pak začnou vytahovat věci z minula co kdo udělal a udělat měl. Nesnaží se pomoci jen ukazují na to jak jsou nejlepší!!!
Offline
#11 29. 05. 2011 13:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: určení těžiště
↑ osshek:
Aby se v tématu "Těžiště" se nerozpoutala debata k Tvé poslední větě, založím pro Tebe (a pro ostatní) speciální téma, ve kterém si můžete vyjádřit svou představu o pomoc. Jinak platí mimo jiné poslední bod pravidel a na ten teď upozorňuji.
Zde prosím řešte jen těžiště. Děkuji.
Téma jsem založila - odkaz.
Offline
#12 29. 05. 2011 13:41 — Editoval LukasM (29. 05. 2011 13:44)
Re: určení těžiště
↑ osshek:
To co máš nahoře zakroužkované (začíná to y(x)=..) - to se dosazuje do obou vzorců za y, a nijak se to neupravuje.
Pokud ti není jasný výraz y(x)=.. jak tam vidím podle těch dvou otazníků, to znamená pouze to, že to číslo za "=" popisuje ypsilonovou souřadnici té paraboly. Ta druhá část ( y(x)=.. ) pouze znamená, že tato ypsilonová souřadnice je popisována v závislosti na proměnné x. Celé se to čte asi "Ypsilon jako funkce proměnné x se rovná ..." To znamená, že je to předpis, jak pro každé x dopočítat hodnotu y.
To nakonec vidíš na tom obrázku. Když vezmeš nějaké číslo na vodorovné ose, a dosadíš do toho "y(x)=.." za x, dostaneš ypsilonovou souřadnici bodu na té parabole.
Ty otázky "Proč?" na pravé straně - protože tak je to v tom vzorci. Se zdeňkem jsme se ti pokoušeli vysvětlit proč ten vzorec vypadá zrovna tak, ale říkal jsi, že o elementech Dx a Dy víš...
Tak, když do těch integrálů dosadíš, zjistíš, že v obou je pouze neznámá x (y jsme už vyjádřili jako funkci x, viz výše), a podle té se má integrovat. Tzn. integrály pak jde spočítat. To, jak píšeš na začátku příspěvku #10, umíš.
A přestaň vykládat o tom jak ti tu ubližujeme. Jen to že tenhle příspěvek vůbec píšu ukazuje, že zas takovej ohava nejsem, protože to dělat vůbec nemusím (v tuhle chvíli popravdě už ani nechci) a nic z toho nemám. A kdybych chtěl na tomhle fóru ukazovat že jsem nejlepší, byl bych pro ostatní (daleko lepší) akorát za blbce.
Kecy o akademických titulech si taky nech, zrovna já osobně mám akorát maturitu (a nepochybuji že spousta ostatních zmiňovaných "akademiků" na tom nebude jinak).
Případnou odpověď na tento odstavec napiš do toho jiného tématu jak píše jelena, já už to nechám tady. Odkaz na to téma: http://forum.matweb.cz/viewtopic.php?id=31830.
Offline
#13 29. 05. 2011 17:19 — Editoval osshek (29. 05. 2011 18:08)
Re: určení těžiště
↑ LukasM: omlouvám se ale vytočilo mě to a dekuji za vysvětlení. S nebyla to cílená provokace jako když jsem zkoušel nervy profesora fyziky a páčil sem z něj co je to Fí u úhlové rychlosti a atd. Prostě mi to nebylo jasne od začátku a nejsem zastáncem učení se něčeho na spaměť čemu nerozumím. A tvrdit že to tak je a budeme tomu věřit. Nechci být jak jedna paní v práci co programuje Laser a neumí zpočítat ručně plochy křivek a tím množství mtr spotřebovaného.
Ono se to ze skrypt dost špatně chápe bez tlumočníka nebo slovníku
 hlavně tady u te plokoule sem z toho jelen
hlavně tady u te plokoule sem z toho jelen 

Offline
#14 29. 05. 2011 22:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: určení těžiště
↑ osshek:
děkuji za vysvětlení, za omluvu a za EDIT - náhled do materiálů. Opravdu by bylo lepší přesně vyznačit konkrétní vzorec, který není jasné.
Jelikož upozorňuješ na příklad "Polokoule", tak snad pomůže, když>
a) si zopakuješ goniometrické funkce úhlů v trojúhelníku,
b) výpočet obsahu trojúhelníku dle vzorce  ,
,
c) fakt, že pro hodně malé hodnoty úhlu (zde je to  ) můžeme nahrazovat sin(úhlu) přímo velikosti tohoto úhlu v radiánech.
) můžeme nahrazovat sin(úhlu) přímo velikosti tohoto úhlu v radiánech.
To bych viděla jako takové momenty, co plynou z předchozí přípravy a nejsou zřejmé přímo z předloženého textu. Případně upřesní. Děkuji.
Offline
#15 12. 06. 2011 14:21
Re: určení těžiště
no tak težíště je uplná španělská vesnice pořád mi není jesné kdyz vezmu element funkce Dx nebo dy a zintegruju tak mam zase tu samou funkci a jek počítam tak počítám pořád mi to nevychází sem asi atvrdlý nebo nevím
Offline
#16 12. 06. 2011 15:10 — Editoval jarrro (23. 08. 2019 20:08)
Re: určení těžiště
↑ osshek:↑ zdenek1:
keďže ide o ťažisko rovinného telesa tak by tam mali v čitateli vystupovať integrály dvojné hustotu môže považovať za konštantnú teda rovnú jednej teda bude![kopírovat do textarea $x_T=\frac{\int\limits_{0}^{H}{\int\limits_{0}^{\sqrt[3]{kx}}{x\mathrm{d}y}\mathrm{d}x}}{\int\limits_{0}^{H}{\sqrt[3]{kx}\mathrm{d}x}}\nl y_T=\frac{\int\limits_{0}^{H}{\int\limits_{0}^{\sqrt[3]{kx}}{y\mathrm{d}y}\mathrm{d}x}}{\int\limits_{0}^{H}{\sqrt[3]{kx}\mathrm{d}x}} $](/mathtex/4c/4caa59d47b80ae091f9a22c54681582a.gif)
y je tu premenná ako každá iná čitatele sú vlastne dvojnásobné integrály z funkcie f(x,y)=x resp. f(x,y)=y cez oblasť určenú ako podgraf tej tretej odmocniny
EDIT vlastne to vypočítaní vnútorného vedie na tie isté jednoduché integrály,ale tam je už y rovné tej tretej odmocnine
MATH IS THE BEST!!!
Offline
#17 12. 06. 2011 17:44 — Editoval osshek (12. 06. 2011 17:49)
Re: určení těžiště
Děkuji Jarrro ale nejsem si jist že to pochopím a zřejmě se to ani nikdy nenaučím. Tak pujdu ke zkoušce a předvedu co sem se ze statiky naučil a budu se modlit ať se mě na to nezeptá a když zeptá tak nevím. Partyzán je proti mě ukecená ženská. Prosím zkuste Ještě jednou a polopatě. ve stylu Vezmeš funkci dosadíš a máš prostě jak pro blbého a zkuste aji s tym integralem
Offline
#19 17. 06. 2011 19:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: určení těžiště
osshek napsal(a):
ne není tam chyba je to takové zadání od dr Hlavačkove do předmětu statika, Taky sem měl něco podobného a nehnul sem stím Je to tady na foru a nakonec sem se na to vybodl a sehnal sem zadání bez těžiště a neučil sem se jej. Jestli mužeš Rumburaku tak nám to vysvětli objema Sme na matiku a tím i na integrál kopyta. Jde o to že nevíme co kam dosadit a co stím dělat. Třeba kolega do mého odkazu dal tohle
a ja to umím akorád tak přečíst. Integrál v matematice sem se nejak po haluzi naučil a předvedl u zkoušky. Prostě polopatě a s ukázkama prosím
jarrro napsal(a):
↑ osshek:veď normálne vypočítaj tie integrály alebo už to ti robí problém? veď sú to úplne základné integrály platí
Offline
#20 18. 06. 2011 00:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: určení těžiště
osshek napsal(a):
Integrál v matematice sem se nejak po haluzi naučil a předvedl u zkoušky. Prostě polopatě a s ukázkama prosím
jelikož materiál paní Hlaváčkové mám uložen na klíčová slova "linecké kytičky", tak jsem ho podrobně prohlédla a máte umět používat pouze určitý integrál (nemáte mít dvojný integrál). A to jste mohli s kolegyňkou Katkou sdělit sami, kolegové by si ušetřili čas.
Určitý integrál s ukázkami předvedl kolega ↑ zdenek1: a doplnil kolega ↑ jarrro:. Jaké jiné ukázky byste chtěli? Určitý integrál - například zde.
Lze téma považovat za vyřešené? Děkuji.
...
Offline
#22 18. 06. 2011 20:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: určení těžiště
↑ osshek:
Ten poslední hudební? Také se mi libí :-) Jinak jako kluk od ponku jsi určitě zvyklý jasně formulovat zdroj problému - příště k tomu tak přistupuj, čím se ušetří čas Tvůj a kolegů.
Děkuji, označím za vyřešené. Ať se daří.
Offline

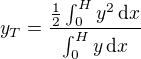
![kopírovat do textarea $x_T=\frac{\int_0^Hx\sqrt[3]{kx}\,\text dx}{\int_0^H\sqrt[3]{kx}\,\text dx}=\frac{\int_0^Hx^{\frac43}\,\text dx}{\int_0^Hx^{\frac13}\,\text dx}=\frac{\frac37x^{\frac73}|_0^H}{\frac34x^{\frac43}|_0^H}=\frac47x|_0^H=\frac47H$](/mathtex/6c/6cc5e2e7c2098461b7994c4d62bb565f.gif)
 je to velmi podobné. Rozřežeš to na sloupečky, u každého sloupečku najdeš střed, ten je v
je to velmi podobné. Rozřežeš to na sloupečky, u každého sloupečku najdeš střed, ten je v  a sloupečku přiřadíš váhu úměrně výšce sloupečku tj.
a sloupečku přiřadíš váhu úměrně výšce sloupečku tj.  .
.