Matematické Fórum

janca361 · 14. 10. 2011 20:38

Zdravím, mám úkol:
Dokažte, že platí $\Delta T = \Delta t$ .
$T$ je teplota v Kelvinech ( $K$ ), $t$ teplota ve $^\circ C$ .

Vím, že platí převodní vztah:
$t=(\{T\}-273,15)^\circ C$
$T=(\{t\}+273,15)K$

Netuším, co se po mně chce. Dokáže mě někdo pošoupnout dát? Děkuji.

frank_horrigan · 14. 10. 2011 20:54

Ahoj,

víme, že Celsiova stupnice vychází z té Kelvinovy, jen "vertikálně" posunutá.

O kelvinově stupnici a jeho jednotce víme: že definována dvěma body, a to absolutní nulou, a teplotou trojnýho bodu vody (273,16 kelvinů)

Dále o stupnicích víme, že absolutní jednotka (stupeň) je u obou shodná. Tehdy tedy platí: $t = T + 273.15$ . Delta T (rozdíl $t_1 - t_0$ je z definice stejného absolutní délky stupně tedy také shodný.

pietro · 14. 10. 2011 21:59

↑ janca361:

janca361 · 15. 10. 2011 16:24

↑ pietro:
No úplně tomu nerozumím. Zkusela jsem to nějak, jak jsem to pochopila...
$\Delta T&=\Delta t \\ T_1-T_2&=t_1-t_2$

$T_1=t_1+273,15 \\ T_2=t_2+273,15$

$T_1-T_2&=t_1-t_2 \\ (t_1+273,15)-(t_2+273,15)&=t_1-t_2 \\ t_1+273,15-t_2-273,15&=t_1-t_2 \\ t_1-t_2&=t_1-t_2$

Sedí to, jen tomu nerozumím. Přece každá stupnice má jiný "dílek". Když stoupne o 1K, není to to samo co o 1°C, nebo se pletu? (Opravdu si to nedokážu představit...)

((:-)) · 15. 10. 2011 16:53

↑ janca361:

Ahoj. Z Wikipédie:

medvidek · 15. 10. 2011 16:53

↑ janca361:
No právě, ten dílek je stejný (z definice).

Pavel Brožek · 15. 10. 2011 17:00

↑ janca361:

Celsiova a Kelvinova stupnice jsou jen různé způsoby, jak zapsat, v jakém stavu je systém. Když někdo chce, abychom dokázali

$\Delta T = \Delta t$ ,

tak po nás chce, abychom ukázali, že pokud máme dva stavy systému, tak jejich teplotní rozdíl v obou stupnicích je číselně stejný.

janca361 · 15. 10. 2011 17:37

↑ ((:-)):

Fyzika pro gymnázia (Karel Bartuška) napsal(a):
Termodynamická teplotní stupnice má jen jednu základní teplotu. Byla za ni zvolena teplota rovnovážného stavu soustavy led + voda + sytá pára. Tento stav se nazývá trojný bod vod a dohodou mu byla přiřazena teplota T_r=273,16K (přesně). Z této dohody vyplývá definice kelvinu jako základní jendotky soustavy SI:
Kelvin je 1/273,16 díl termodynamické teploty trojného bodu vody.

To jen pro opravdu Wikipedie.

K té definici: Z čeho to vychází?

↑ Pavel Brožek:
Tak teď už tomu nerozumím vůbec :( Dokázala jsem něco nebo ne?

Pavel Brožek

↑ janca361:

(Číselné hodnoty bez jednotky značím složenými závorkami.)

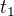Máme systém ve stavu 1. V Kelvinově stupnici má teplotu $T_1$ . Jaká bude jeho teplota $t_1$ ve stupních Celsia?

$\{t_1\}=\{T_1\}-273,15$

Dále máme systém ve stavu 2. V Kelvinově stupnici má teplotu 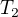$T_2$ . Jaká bude jeho teplota $t_2$ ve stupních Celsia?

$\{t_2\}=\{T_2\}-273,15$

Teplotní rozdíl mezi stavem 1 a 2 vyjádřený v Kelvinově stupnici je

$\{T_2\}-\{T_1\}$ .

Teplotní rozdíl mezi stavem 1 a 2 vyjádřený v Celsiově stupnici je

$\{t_2\}-\{t_1\}=(\{T_2\}-273,15)-(\{T_1\}-273,15)=\{T_2\}-\{T_1\}$ .

Tím jsme dokázali, že číselná hodnota teplotního rozdílu je v obou stupnicích stejná.

(V podstatě to napsal už Pietro, ale bez komentáře. Ty jsi postupovala nějak obráceně, nejprve píšeš, že se rozdíly rovnají a pak dojdeš k evidentně pravdivému tvrzení $t_1-t_2=t_1-t_2$ . Kdyby jsi šla od konce, tak to bude důkaz.)

Když stoupne o 1K, není to to samo co o 1°C, nebo se pletu?

Když řekneme, že teplota stoupla o 1K nebo o 1°C, tak to je to samé.

medvidek · 15. 10. 2011 18:14

Asi před rokem jsem zde napsal:

Nedávno jsem si prohlížel učebnici termiky pro SŠ (vydavatelství Prometheus) a měl jsem dojem, že se někdo snažil naházet na hromadu různé informace s tím, že dobrý student (nebo učitel) si už něco vybere. Kromě toho například první odstavec kapitoly 1.7 "Termodynamická teplota" jsem "nepobral", ani když jsem ho přečetl nejméně pětkrát. Co z toho základu si asi může vzít student?

Tuto učebnici již doma nemáme, tak nevím, zda je od Karla Bartušky.

janca361 · 15. 10. 2011 22:40

↑ medvidek:
Ano, je to ona.

janca361 · 16. 10. 2011 12:35

↑ Pavel Brožek:
Jak jsem šla od konce?
Mám dokázat, že platí: $\Delta T&=\Delta t$ , co je $T_1-T_2&=t_1-t_2$ . Vyjádřím si Kelvinovu teplotu v Celsiově: $T_1=t_1+273,15$ $T_2=t_2+273,15$
Dosadím to za $T_1-T_2&=t_1-t_2$ : $(t_1+273,15)-(t_2+273,15)&=t_1-t_2$ a upravím:
$t_1+273,15-t_2-273,15&=t_1-t_2 \\ t_1-t_2&=t_1-t_2$

Mě to teda připadá stejný jako to tvoje. Možná moje chyba je v tom, že vycházím, že je to pravdivé (bylo mi to řečeno a věřím, že je). Možná, kdybych to nevěděla, tak postupuju jinak.

↑ medvidek:
Ještě k té učebnici. Mechanika z té řady byla skvělá, ale Molekulová fyzika a termodynamika nic moc. Možná je to tím, že je to spíš teorie.

Pavel Brožek

↑ janca361:

Když něco dokazuješ, nemůžeš vycházet z toho, co dokazuješ. Pokud máme výrok, který chceme dokázat $V$ (v tomto případě výrok V je $T_1-T_2&=t_1-t_2$ ) a výrok, který je evidentně pravdivý $A$ (v tomto případě $t_1-t_2&=t_1-t_2$ ), chceme ukázat implikaci $A\Rightarrow V$ , ne $V\Rightarrow A$ (to jsi udělala ty). Pokud jsou ale všechny úpravy ekvivalentní (tj. v tvém případě $V\Leftrightarrow B_1\Leftrightarrow B_2\Leftrightarrow\ldots\Leftrightarrow A$ , kde B jsou nějaké výroky, přes které postupujeme k výroku A), tak si z toho můžeme „vybrat“ ty šipky vlevo ( $V\Leftarrow B_1\Leftarrow B_2\Leftarrow\ldots\Leftarrow A$ ), otočit pořadí ( $A\Rightarrow\ldots\Rightarrow B_2\Rightarrow B_1\Rightarrow V$ ) a máme důkaz $A\Rightarrow V$ .