Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limit posl., lim. fnc., integral... (TOTO TÉMA JE VYŘEŠENÉ)
#26 29. 08. 2008 09:04 — Editoval Olin (29. 08. 2008 09:04)
Re: Limit posl., lim. fnc., integral...
jelena napsal(a):
Kdyz vidim důkaz kolegy ↑↑ BrozekP:, tak bych si už dovedla představit i odvozování vzorce od druhé pozoruhodné limity.
Pochopil jsem z toho správně, že jde o limitu  ? Na tu jsem vymyslel krásný důkaz. Ve skutečnosti jsem ho objevil už před léty, ale teprv nedávno jsem si uvědomil souvislost s touto limitou.
? Na tu jsem vymyslel krásný důkaz. Ve skutečnosti jsem ho objevil už před léty, ale teprv nedávno jsem si uvědomil souvislost s touto limitou.
Dá se jednoduše kombinací pár vzorců odvodit, že pro obsah pravidelného n-úhelníka platí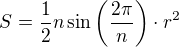 ,
,
kde r je poloměr kružnice opsané. Jestliže jde n k nekonečnu, musí se tento n-úhelník přibližovat kružnici, pro kterou platí .
.
Tedy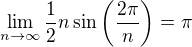
Odtud substitucí 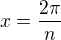 a požadavkem
a požadavkem 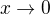 dostáváme chtěnou limitu.
dostáváme chtěnou limitu.
Všechno poměrně jednoduchá SŠ matematika ;-)
Offline
#27 29. 08. 2008 11:40
Re: Limit posl., lim. fnc., integral...
ja ty postupy vsecky beru nekde po netu..jak mi tady doporučuje slečna Jelena..jo mimochodem tohle jsou příklady z zkouškových testu na mé škole...mame tam matiku něco jako cedník..3 mesice se teprv snazim tyhle vsecky veci pochopit a nejak se pořad nedaří..všem děkuju za pomoc..ty postupy vlastne některy jsou jeste od naseho pana učitele, prej je dost známej ve světě Luděk Jirkovsky..ale podle mě už tu matiku učí moc dlouho.neda se snim ani mluvit..
Offline
#28 29. 08. 2008 16:35
Re: Limit posl., lim. fnc., integral...
↑↑ jelena: tak že ten integrál z té 11 bude asi takhle?:) http://forum.matweb.cz/upload/714-11_4.JPG
Offline
#29 29. 08. 2008 16:45
Re: Limit posl., lim. fnc., integral...
mám tu ješte dvě podobnou limitu zkoušel sem to vašim způsobem a vy šlo mi e^(pí^2/x)
ale do postupu jsem se uplně zamotal, tak nějak nevim jak jsem k tomu došel:D a u ty druhy limity, nemam tuch ajk ji počitat s tímto typem sem se ještě nesetkal.. http://forum.matweb.cz/upload/621-33_1_2.JPG
Offline
#30 29. 08. 2008 17:05 — Editoval kaja.marik (29. 08. 2008 17:07)
#31 29. 08. 2008 17:35
Re: Limit posl., lim. fnc., integral...
↑ kaja.marik: tak misto x ma bejt "n" ..myslel sem si že to bude tajta věta, takže je to nula pohoda, děkuju ale tu první proste nemužu na to přijit
Offline
#32 29. 08. 2008 18:08
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Limit posl., lim. fnc., integral...
ve vysledku neni nikdy ta promena, ktera se v limite nekam blizi.
Zkuste sem napsat sve myslenkove pochody, aby vam nekdo mohl dat vedet, kde delate chybu. Vysledek si muzete overit online na mnoha mistech internetu, ale dulezitejsi je postup.
Offline
#33 29. 08. 2008 20:59 — Editoval jelena (30. 08. 2008 14:51)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ kaja.marik:
↑ bons:
1. Výsledek integrování je v pořádku (nezapomeň připsat na závěr +C), můžes si ho ověřit také "ručně", když výsledek zderivuješ.
2. při vypočtu této limity se používá vztahu, který má uveden třeba BrozekP v příspěvku 20.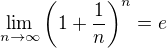 , ovšem je potřeba zápis zadání trochu upravit, aby bylo možné použit uvedený vztah:
, ovšem je potřeba zápis zadání trochu upravit, aby bylo možné použit uvedený vztah:
je to srozumitelne, co dělám a jak to dopadne?? - tento postup by měl byt uveden v materialech z cviceni
3. pro pořádek v posledním zadání s lim - rozumíš tomu, proč kaja.marik rika, že funkce sin (pi/x) pro x jde do 0 je ohraničena? Stači i polopatický názor, děkuji :-)
Offline
#34 29. 08. 2008 21:48 — Editoval jelena (30. 08. 2008 13:09)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
Ted ještě odpovím na otázky vážených kolegů :
↑ Olin:
já jsem měla na mysli 2. pozoruhodnou limitu - s "e" ve výsledku. Tvůj důkaz neumím posoudit, jak jsem říkala, není to moje silna stranka - snad někdo z opravdových matematiků.
---------------------------------------------------------------
Pro Kaju Marika - jak jste si vsiml, na Východě a u techniku máme vsechno presně pojimenované a jednotlivé vzorce se takto učí - pak se cvicilo a porad se ríkalo, co za vzorec, nebo zákon, nebo větu pouzili.
-------------------------------------
Vidite: - náš kolega emco - bons to sám říka - na technikach a zřejmě i přirodovědach se používá matematika jako cednik. Použití kuchařky je tedy zcela na místě :-)
Kolega bons by si zasloužil nějakou přiměřenou výchovnou poznámku, ale pro dnešek už jsem toho napsala dost, nekdy jindy. Věřím, že to půjde dál lépe, než dosud :-)
bons napsal(a):
jak mi tady doporučuje slečna Jelena...
čístě pro pořádek - ne, že bých si zakladala na nějakem titulování, ale preferuji buď mé forum - jméno "jelena" nebo skutečné jméno Jelena (můžete, kdo vysloví, i v původním znění Елена Игоревна), ale tu slečnu, prosím, to nechte někám do pokladny :-)
-----------
Bohužel, nemáme poslední dobou čtení na pokračování, doufám, že se k tomu opět dostaneme.....
slabou útěchou bude úvodní lekce do matematiky v ruštině.
Offline
#35 30. 08. 2008 14:28
Re: Limit posl., lim. fnc., integral...
↑ jelena: tak já to řešil takhle ale to asi bude špatně:) http://forum.matweb.cz/upload/531-mat008.jpg
k tý druhy limitě to x pod tou odmocninou jde k nule a ten zbytek do nekonečna tak proto to je?:)
Offline
#36 30. 08. 2008 14:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
Pro bons, zdravím :-)
1.
bons napsal(a):
toto je úplně v pořádku, mám stejný postup, jen jsem měla malý preklep v zadání, uz je opraveno.
2.
bons napsal(a):
k tý druhy limitě to x pod tou odmocninou jde k nule a ten zbytek do nekonečna
x pod odmocninou jde k 0 - souhlas
z vlastností funkce sin víme, že je ohraničena (obor hodnot je v intervalu <-1, 1>), pi/x jde k nekonečnu pro x jdoucí k 0, sin (pi/x) je ohranicena.
Pro násobek lze tedy pouzit větu, jak odkazuje kaja.marik
OK?
Offline
#37 30. 08. 2008 15:14 — Editoval bons (30. 08. 2008 15:26)
Re: Limit posl., lim. fnc., integral...
↑ jelena: fýha..tak to koukám, že sem to da spravně:D dik za vysvětlení:) vedu si sešit a ten se pěkně plní:D každopadně sem zkoušel počítat dál a mam tady další sadu příkladu...
http://forum.matweb.cz/upload/464-7_3.jpg tady to by mělo bejt snad v pořadku..ale stoprocentní jistotu nemam:) tady jen to vyšetření křivky to druhy ne.. http://forum.matweb.cz/upload/387-9_3.JPG jěšte sem se chtěl zeptat jestli u tady toho příkladu musí bejt načrt.. http://forum.matweb.cz/upload/344-15.jpg tady mam 4 příkladky první limita by měla bejt v pohodě,druha ta nakonci to jsem se krapet zamotal.. 3 příklad tam ta nejmenší hodnota ty funkce to si nejsem jistej a integral sem se zamotal..:D
ps: Jelena, omlouvám se za tu slečnu...moc si cením vaší pomoci..snažím se učit co to dá..
Offline
#38 30. 08. 2008 18:04 — Editoval jelena (30. 08. 2008 18:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
Zdravím .-)
nikdo z kolegu není online :-(
tak alespoň v rychlosti:
první úloha (s parabolou) OK, je tam malý překlep - pod odmocninou má byt ... +3, ale na celkový výsledek to nemá vliv.
druhá úloha - vyšetření křívky:
(tady jsem editovala, dobrá chybá byla - moje :-)
úpravy jsou provedeny pro x není 0, vyšetření je v pořádku, ale na můj pohled není úplné:
- obvyklé je ještě třeba sudost - lichost, průsečíky s osou x, y, vyšetření kovexnosti a konkávnosti, asymptot (chtělo by vědět, zda učitel požaduje). Náčrt je opravdu vhodný.
Test 15.
1) limita - použití l´Hospital pro posloupnost bez dalších upřesnění není úplně vhodné, možná, že v materálech máte, co se musí napsat, aby se dálo použit - výsledek bude úplně stejný, ale podmínka pro použití musí být napsána.
Na foru se to už diskutovalo - pohledám odkaz http://forum.matweb.cz/viewtopic.php?id=375
2) limita - ošklivá :-) bude se to hledat převodem na zápis e na ln(celeho toho výrazu, co je zadán) - je potřeba hodně pozorně provést úpravy pomocí právidel počítaní s ln
Zkus nejdřiv pořádně rozepsat ln (.... všeho, co je napsáno po lim). Pak se ozví, OK?
3) funkce arctg - všechno v pořádku, pouze druhý zlomek (úplně první derivace) musí mít v čitateli (-1) - je tam derivace složené funkce (1-x), ale v další úpravě už to je, zřejmě jen překlep.
Vyšetření nalezeného bodu - zda je to max, doporučuji pomocí změny znamenka derivace před a po x=0 (stačí dosadit třeba - 0,5 a 0,5 do výrazu pro derivaci) a doložit, že funkce je rostoucí pro x od -1, do 0 a klésající na 0, +1. Z tohoto uz lze udělat závěr, že to je max hodnota na celém intervalu. a min hledat v okrajových bodech.
f(0) = arctg 1 + arctg 1 = pi/4 + pi/4 = pi/2
(90, co máš zapsáno - jsou stupně, to ovšem težko zakreslime na číselnou osu, až budeme kreslit náčrt) - pro jistotu, kde je na číselné ose pi/2?
f(1) = arctg (2) + arctg (0) = arctg (2) +0 = arctg (2) - opět přes radiany, ne přes stupně,
f(-1) = arctg (0) + arctg (2) = (0) + arctg (2) = arctg (2) - opět přes radiany, ne přes stupně.
4) Integrál - metoda per partes, bude použita 2 krat:
t^2 = u'
ln^2 (2t) = v
Mělo by to vyjit po 2. kroku.
Doufám, že někdo z kolegu to překontroluje (co já vím, co je možné napsat s vysavačem v ruce :-), děkuji.
Hodně zdaru :-)
Offline
#39 30. 08. 2008 19:34
Re: Limit posl., lim. fnc., integral...
↑ jelena: tak zatim z tý 15ctky jsem opravil 2 a 3:) tak snad jsem zvolil dobrý postup http://forum.matweb.cz/upload/149-test15.jpg
Offline
#40 30. 08. 2008 21:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ bons:
k vyšetření funkce s arctg nebylo potřeba nic zásadního měnit:
v bode x=0, y= arctg(1) + arctg(1)=pi/2 skutečně nastává maximum funkce, minimum nastává pro hodnoty x = -1, 1 k těmto hodnotam dopočitáme f(x) - jak uvádím ve svém příspěvku.
limita - v původním zadání je x -> nekonečnu (teď máš ale k 0), asi překlep, jinak úpravy jsou v pořádku.
Prosím nekoho z kolegů překontrolovat, zda je to správný postup - nejsem si tak úplně jista, zda ln(cos(x))/x^4 pro x se bliží nekonečnu můžeme považovat za 0, nebo je nutná ještě nějaká úprava, děkuji :-)
Offline
#41 30. 08. 2008 22:19 — Editoval kaja.marik (30. 08. 2008 22:24)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Limit posl., lim. fnc., integral...
jelena napsal(a):
↑ bons:
ln(cos(x))/x^4 pro x se bliží nekonečnu můžeme považovat za 0
Podle mne takova "limita" nema smysl. V kazdem okoli nekonecna najdu body nepatrici do definicniho oboru a limitu nemuzu pocitat. Asi tam ma byt opravdu x jdouci k nule.
↑ bons: U te limity, ta poznamka v pravem hornim rohu, ze x je libovolne nenulove realne, je spatne. Je-li exponent realne cislo, musi byt zaklad mocniny kladny.
----------------------------------------------
Prázdniny, které následovaly po prvním roce studií Káji a Zdeni v Praze, byly ty nejkrásnější, jež si lze pomyslit. A proto uběhly tak rychle. :(
Offline
#42 30. 08. 2008 22:38 — Editoval BrozekP (30. 08. 2008 23:04)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limit posl., lim. fnc., integral...
↑ jelena:
Nečetl jsem téměř nic z toho co tu teď řešíte, je to moc úloh najednou a to nemám rád :-). Ale všiml jsem si žádosti o kontrolu, tak se k tomu vyjádřím:
Označím 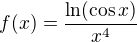 , v bodech kde není definovaná ji libovolně dodefinujeme. Je zřejmé, že pro posloupnost
, v bodech kde není definovaná ji libovolně dodefinujeme. Je zřejmé, že pro posloupnost  je
je 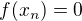 a tedy
a tedy 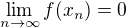 . Proto pokud limita funkce f v nekonečnu existuje, pak je podle Heineho věty rovna nule. Ukážu ale jinou posloupnost a_n jdoucí do nekonečna, pro kterou
. Proto pokud limita funkce f v nekonečnu existuje, pak je podle Heineho věty rovna nule. Ukážu ale jinou posloupnost a_n jdoucí do nekonečna, pro kterou 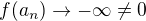 , čili podle Heineho věty limita
, čili podle Heineho věty limita 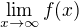 neexistuje. Takovou posloupností je například
neexistuje. Takovou posloupností je například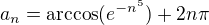 , protože
, protože
EDIT: upraveno, aby bylo v souladu s ↑ kaja.marik:
Offline
#43 30. 08. 2008 23:01 — Editoval kaja.marik (30. 08. 2008 23:07)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Limit posl., lim. fnc., integral...
↑ BrozekP:
Definice limity casto zacina slovy "necht funkce je definovana v ryzim okoli bodu c", nebo tak neco, viz napr.
formalni definice limity na wikipedii
Pokud ne, tak se aspon rika ze musi existovat delta takove, ze plati nerovnost |f(x)-L|<epsilon pro vsechna x splnjici 0<|x-c|<delta ( viz http://mathworld.wolfram.com/Limit.html ). Aby ta nerovnost platila, tak zejmena musi mit smysl a zase mame, ze funkce musi byt definovana v nejakem ryzim okoli bodu c. Tohle je vlastni bod, v nevlastnich bodech to je analogicke.
Nekdy se pouziva slabsi definice limity, kdy staci aby bod ke kteremu se limitne blizime byl hromadnym bodem definicniho oboru, ale nepredpokladam ze toto je nas pripad.
-----------------------------------------------------
Jemu by se jen vysmála, ale a? těch ženichů přivezou Zdeně třeba pět, ani jeden z nich nebude ji mít tak rád jako on, Kája! Vždycky! I když bude už třeba ve Vídni, pořád ji bude mít rád. Jen když ona nebude o tom vědět, aby se mu nevysmála!
Offline
#44 30. 08. 2008 23:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
OT:
↑ kaja.marik:
Zdravím Vás :-)
my už nečteme z prvního dílu, je to tak? :-) ale jsem moc rada, že čteme :-)
-----------------------------------------
↑ kaja.marik:, ↑ BrozekP:
Hezký večer, já vás nechávám s problémem, nebo? už se nechytám :-)
Moc děkuji, že jste se podivali - já se přiznám, že jsem z té limity zmatena - asi počkáme na kolegu, co platí - x k nekonečnu nebo k 0.
Máte pravdu s přerušovaným def. oborem pro ln(cosx) pro x k nekonečnu, ale s x k nule jsem ještě nekontrolovala, nemám bohužel moc času.
Myslím, že u ostatních zadání to je běžná klasika, ale opět máme limitu od
bons napsal(a):
od naseho pana učitele, prej je dost známej ve světě Luděk Jirkovsky
Ostatně, nápad, že budeme kontrolovat, vymyslel Marian, hm...
Offline
#45 30. 08. 2008 23:06
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limit posl., lim. fnc., integral...
↑ kaja.marik:
Děkuji, nedalo mi to a trochu jsem hledal a dospěl ke stejnému, takže jsem svůj příspěvek upravil dodefinováním funkce.
Offline
#46 30. 08. 2008 23:29 — Editoval kaja.marik (31. 08. 2008 00:45)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Limit posl., lim. fnc., integral...
↑ jelena:
OT: Take zdravim :) Priznavam ze jsem forum zanedbaval, protoze jsem mel furu prace s dovolenou, s prazdninama a s odpocivanim a relaxaci :)
Tady vlastne relaxuji :-) - nebot v zamestnani a v rodine musim porad plnit pozadavky ostatnich, ale tady si mohu vybirat a reagovat pouze na to, na co se mi chce :-) Jeste moc rada relaxuji u umyvani nadobi :-)
Pokud jsem odpovidal tak to byvalo jenom narychlo. Vetsinou jsem jenom cetl a nepsal. Ale forum mi i tak dalo hodne, napriklad
1. Videl jsem zajimave prazdninove priklady
2. Vsiml jsem si, ze pravdepodobne krome Joricy osobne znam jeste jednoho clena osazenstva
3. Zaradil jsem krajinarum do prednasek numerickou metodu zalozenou na Banachove vete, protoze jenom pulit interval je nuda - viz vlakno http://forum.matweb.cz/viewtopic.php?id=3716
----------------------------
Protoze tento prispevek je silne off topic, tak pridavam misto cteni na pokracovani odkaz, ktery matematicke snazivce snad rozesmeje stejne jako me: vypatlátor
Offline
#47 31. 08. 2008 00:56
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limit posl., lim. fnc., integral...
jelena napsal(a):
limita - v původním zadání je x -> nekonečnu (teď máš ale k 0), asi překlep, jinak úpravy jsou v pořádku.
K nule to vychází hezky, takže s nulou to bude to správné zadání
↑ bons:
V té limitě v příkladu 2 máš v posledním kroku chybu, před ln(cos x) má být 4, ne 2. Dále se pak dá postupovat například L'Hospitalem.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limit posl., lim. fnc., integral... (TOTO TÉMA JE VYŘEŠENÉ)