Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Kombinatorika 2 (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 10. 2013 19:34
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Kombinatorika 2
Ahoj všichni! Prosím o radu s příkladem:
Chceme vedle sebe do řady postavit 5 dívek a 7 chlapců, přičemž nesmí vedle sebe stát 2 dívky (stále mezi sebou štěbetají). Kolik máme možností?
Ať se snažím, jak se snažím, nějak mi to pořád nedochází :D
Moc děkuji za rady, Katsu
Offline
- (téma jako vyřešené označil(a) Katsushiro)
#2 16. 10. 2013 10:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika 2
Zdravím,
budu alespoň udržovat společenskou konverzaci (když už jsem ideová tetuška sekce), než se dostaví někdo zdatnější. Je mi jasné, že půjde hlavně o zaplnění mezer mezi dívky (mezer je celkem 4 "povinných" - tak vyčerpáme minimálně 4 chlapce)+ můžeme využit pozice před a po dívčím řadu. Do mezer mezi dívky můžeme dávat i více kluků.
Tak bych začínala rozestavením dívek (nevhodných elementů). Ale v příkladů 2.11 pan Kubesa začíná umístěním elementů vhodných. Zkoušel jsi projít tento příklad? Děkuji.
Offline
#3 16. 10. 2013 15:24
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Kombinatorika 2
↑ jelena:
Moc děkuju, tohle jsem nějak přehlédl :D
Zkusil jsem tedy postupovat stejně:
Nejprve rozestavím kluky s mezerami -> 7! , 9 mezer (beru i místo před a za řadou kluků)
Protože mám 5 holek, zbudou mi 4 neobsazené mezery -> mám  možností výběru.
možností výběru.
No a nakonec prohážu holky mezi sebou -> 5!
Takže mám 7! * 126 * 5! = 76 204 800
Není to nějak moc? :D
Offline
#4 16. 10. 2013 15:28
Re: Kombinatorika 2
↑ Katsushiro:
Doporučuju ještě jednou přepočítat mezery mezi chlapci.
Jinak je to OK.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 16. 10. 2013 18:10
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Kombinatorika 2
↑ zdenek1:
Ha, to není možné :D
Samozřejmě máš pravdu, má to vypadat takhle:
Mezer mezi chlapci je 6 + 2 místa po okrajích jejich řady, tj. celkově 8, nikoliv 9 :D
Správné řešení příkladu je tedy:
7! *  * 5! = 5040 * 70 * 120 = 42 336 000
* 5! = 5040 * 70 * 120 = 42 336 000
Moc díky všem za rady ;-)
Offline
#6 17. 10. 2013 23:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika 2
↑ Katsushiro:
také děkuji (a hlavně kolegovi Zdeňkovi, že se zapojil). Rada bych viděla vysvětlení, proč kolega Kondr používal jiný postup, děkuji, nehoří.
Katsushiro v jiném tématu napsal(a):
Ha, zadání mi tlumočil spolužák, evidentně mě mystifikoval :D
:-) víš, co sil a prostředků bylo vynaloženo na tento projekt? A přesto jste pořád ve stavu ústních bájí. Aktuální odkazy přidám do úvodního tématu sekce (pravděpodobně zítra).
Offline
#7 05. 11. 2013 18:26
Re: Kombinatorika 2
↑ jelena:
Kondr
Nejprve rozmístíme 5 mužů a 3 ženy naprosto libovolně (variace s opakováním). Pak tam doplníme zbylé 4 ženy - první napravo od prvního muže zleva, druhou napravo od druhého, ... to už lze jediným způsobem.
Takže můj způsob dává 
a nyní Kondr.
Jeho návod je velmi stručný a předpokládá, že ženy a muži jsou nerozlišitelní. Což je jistě špatně.
Pokud provedem opravu na rozlišitelnost lidí, tak
a) musíme ty ženy nejprve vybrat, to lze 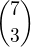 způsoby.
způsoby.
b) přidáme 5 mužů a rozestavíme, to lze  způsoby.
způsoby.
c) rozmístíme zbylé 4 ženy způsobem alá Kondr, jenže když jsou rozlišitelné, jde to udělat  způsoby a nikoli jedním
způsoby a nikoli jedním
Takže dostáváme
Pokud kombinační čísla rozepíšeš, zjistíš, že oba výrazy jsou shodné.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#8 08. 11. 2013 14:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika 2
↑ zdenek1:
Zdravím a děkuji velice, mně ani tak nešlo o to, že výrazy jsou shodné nebo ne, ale o sled úvah, pokoušela jsem se zorientovat v každém ze zadání (i v těchto). No snad už ano :-), kolegovi Kondrovi přidám odkaz na toto téma.
To má zřejmě nějaký metodický smysl, že všude je 5 a 7.
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Kombinatorika 2 (TOTO TÉMA JE VYŘEŠENÉ)