Matematické Fórum

Sharja · 01. 04. 2017 11:16

Ahoj,
v písemce na pravděpodobnost jsme dostali tento příklad: "V šatně je 6 kabátů a šatnářka potmě vydá kabát 4 lidem. Jaká je pravděpodobnost, že nikdo nedostal svůj kabát?"
Učitel to řešil tak, že zkrátka vypsal všechna rozdělení, která vyhovují. To mi přijde opravdu hloupé, když vezmu v úvahu, kolik těch možností je (výsledek má prý vyjít 362/720).
Kromě toho by mě zajímalo, jak by to vypadalo s obecnými hodnotami pro m kabátů a n lidí, což se tak rozepsat nedá.
Netušíte tedy někdo, jak by se to dalo vyřešit?

misaH · 01. 04. 2017 12:11

↑ Sharja:

A čo z kombinatoriky vieš?

Sharja · 01. 04. 2017 13:57

V podstatě to, co se učí na střední... Kombinační číslo, nějaké základní vzorce...

Sharja · 04. 04. 2017 22:15

Máte někdo nějaký nápad, jak by se to dalo vyřešit? Klidně nějakými složitějšími větami, cokoliv kromě vypisování 362 možností :D

jelena · 05. 04. 2017 23:40

Zdravím,

↑ Sharja: můžeš se podívat po "problém šatnářky" nebo "problém sekretářky" (i zde na fóru, např. pohledat "klobouky"). Vaš pan učitel asi zvolil nějakou úspornější metodu, než aby vypsal všech 362 možností (jak prakticky k tomuto číslu došel?).

Mně to vyšlo jinak, ale nejspíš mám nějakou chybu v úvaze. Předpokládám, že je 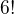$6!$ možností jak umístit 6 kabátů na věšák a předpokládám, že nejdřív kabáty návštěvníků byly na pozicích 1, 2, 3, 4 (návštěvníci mají v kapsách příslušní šatní kolečko, se kterým dojdou pro kabát). Musíme zajistit, aby na "správné" pozici nevisel "správný" kabát.
opět vycházím z toho, že všech umístění je 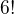$6!$ , odečtu, když kabáty jsou na svých místech:
- na svém místě je číslo 1 (to je $5!$ ),
- na svém místě je 2 (to je také $5!$ , ale ještě 2 byla na svém místě i ve $4!$ případech, když byla na svém místě také 1),
- na svém místě je 3 (to je také $5!$ , ale ještě 3 byla na svém místě (viz odůvodnění pro 2)
....
a tak dojdu k zápisu Odkaz, což je ovšem $326/720$ (ne výsledek, který udáváš). Poprosím kolegu Stýva, aby pokritizoval :-), ale i za kritiku dalších kolegů budu vděčná.

Stýv · 06. 04. 2017 07:49

pomocí principu inkluze a exkluze jsem došel k 181/360 = 362/720

jelena · 06. 04. 2017 10:34

↑ Stýv:

děkuji, kolego Stýve, o to jsem se pokoušela také. Uvažuji alespoň trochu smysluplně, nebo zcela zcestně - ↑ příspěvek 5:? Večer bych popř. doplnila podrobněji. Děkuji a zdravím.

Stýv · 06. 04. 2017 18:27

↑ jelena: Tak to bych nepoznal. Dle PIE se počítá tak, že:
vezmu počet všech možností: 6!
odečtu ty, kde je 1 (4 možnosti který) určitě správně: - 4 * 5!
přičtu ty, kde jsou 2 (C(4,2)=6 možností které) správně: + 6 * 4!
odečtu ty, kde jsou 3 (4 možnosti které) správně: - 4 * 3!
přičtu ty, kde jsou 4 správně: + 1 * 2!

celkem tedy 6! - 4 * 5! + 6 * 4! - 4 * 3! + 2! = 362

Sharja · 06. 04. 2017 18:30 — Editoval Sharja (06. 04. 2017 18:53)

Děkuji za rady. Podle principu inkluze a exkluze mi také vyšlo 362.
Jak jsem k tomu došla:
Pokud je špatně jeden kabát, jsou 4 možnosti, který to bude (A, B, C, D) a počet kombinací pro každý z nich je 5!
Pokud jsou špatně dva kabáty, je 6 možností (AB, AC, AD, BC, BD, CD) a počet kombinací pro každý je 4!
Pro tři kabáty jsou 4 možnosti (ABC, ABD, ACD, BCD), počet kombinací 3!
Pro 4 kabáty je jen 1 možnost a 2! kombinace.

Výsledek by tedy měl být $6!-5!*4+4!*6+3!*4+2!=362$ .

↑ jelena: Myslím, že máš rozebraných moc málo případů. Např. 3 byla na svém místě ve 4! případech, kdy i 1, ale i ve 4! případech, kdy i 2, tím pádem musíš zase přičíst těch 3! případů, kdy byly na svém místě 1, 2 i 3, které jsi odečetla dvakrát.

↑ Stýv: Aha, o dvě minuty později :)

Takže obecně, pro $m$ kabátů a $n$ lidí by výsledek vyšel takto?
$m!-{n\choose 1}*(m-1)!+{n\choose 2}*(m-2)!-{n\choose 3}*(m-3)!+\ldots {n\choose n}*(m-n)!$

Trochu mimo téma: Myslíte si, že je v pořádku dát tuto úlohu do písemky, kde se všechno ostatní dá nakreslit (např. počítání pravděpodobnosti nějakého výsledku, když třikrát hodíme mincí), a to ani ne jako bonusovou? Vzorové řešení od učitele bylo následující: Žádný kabát nesmí být na svém místě. To znamená, že na místě A můžou být jen kabáty B, C, D, E, F. Pokud na místě A bude kabát B, pak na místě B mohou být kabáty A, C, D, E, F. Pokud na místě B bude kabát A, pak na místě C mohou být kabáty D, E, F. V případě kombinace BAD je to tedy 6 možností, v případě BAE 4 možnosti, v případě BAF také 4. A takhle postupujeme dál, než se dopočítáme do oněch 362...

jelena · 09. 04. 2017 00:24

↑ Stýv:, ↑ Sharja: děkuji a pozdravy. Ve ČT se mi to nepodařilo dokončit, pořád mi to nevycházelo a už bylo pozdě, ale snad už ano, doplním, co jsem vynechala:

na svém místě je 3 (to je také $5!$ , ale ještě 3 byla na svém místě (viz odůvodnění pro 2)

- na svém místě je 3 (to je také $5!$ , ale už v předchozím pro 1, 2 bylo započteno, že 3 byla na svém místě, když také byla 1 (4!) nebo když byla na svém místě 2 (4!), tím ale vynechám možnost, kdy na svém místě jsou zároveň 1, 2, 3 ( $3!$ ), přičtu. Tedy pro 3 na svém místě mám $(5! -2\cdot 4!+3!)$

- na svém místě je 4 (to je také $5!$ , ale už bylo započteno, že 4 byla na svém místě, když také byla 1 (4!) nebo když byla na svém místě 2 (4!), nebo když byla 3 (4!), tím ale vynechám možnost, kdy na svém místě jsou zároveň 1, 2, 4 nebo 2, 3, 4 nebo 1, 3, 4 ( $3!$ ), přičtu. A odečtu možnost, když jsou na místě 1,2,3,4 (2!). Tedy pro 4 na svém místě mám $(5! -3\cdot 4!+3\cdot 3!-2!)$ .

Počet všech pozic, kdy žádný z kabátů 1,2,3,4 není na svém místě (snad i shodně s kolegou Stývem):
$6!-(5!+(5!-4!)+(5! -2\cdot 4!+3!)+(5! -3\cdot 4!+3\cdot 3!-2!))=6!-4\cdot 5!+6\cdot 4!-4\cdot 3!+2!$

Sharja napsal(a):
Výsledek by tedy měl být $6!-5!*4+4!*6+3!*4+2!=362$ .

Nějak se neshodujeme a nedává to ani 362 :-(

Zcela mimo téma: již delší dobu pozoruji, že kolega Stýv zásadně změnil svůj způsob užití tečky ve větě :-)

Matematické Fórum

#1 01. 04. 2017 11:16

Pravděpodobnost – šatna ve tmě

#2 01. 04. 2017 12:11

Re: Pravděpodobnost – šatna ve tmě

#3 01. 04. 2017 13:57

Re: Pravděpodobnost – šatna ve tmě

#4 04. 04. 2017 22:15

Re: Pravděpodobnost – šatna ve tmě

#5 05. 04. 2017 23:40

Re: Pravděpodobnost – šatna ve tmě

#6 06. 04. 2017 07:49

Re: Pravděpodobnost – šatna ve tmě

#7 06. 04. 2017 10:34

Re: Pravděpodobnost – šatna ve tmě

#8 06. 04. 2017 18:27

Re: Pravděpodobnost – šatna ve tmě

#9 06. 04. 2017 18:30 — Editoval Sharja (06. 04. 2017 18:53)

Re: Pravděpodobnost – šatna ve tmě

#10 09. 04. 2017 00:24

Re: Pravděpodobnost – šatna ve tmě

Sharja napsal(a):

Zápatí