Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 06. 2021 12:25
Algebra Lagrangeova věta
ahoj potřeboval bych pomoct.
mám pomocí důsledku L věty : "V konečné grupě je řád každého prvku dělitelem řádu grupy" ukázat že každá grupa řádu 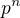 , kde p je prvočíslo, má podgrupu řádu p.
, kde p je prvočíslo, má podgrupu řádu p.
Tady je odkaz na skripta
ze kterých to je, strana důsledku je 42 (7.9) a příklad je na straně 44
Předem díky
Offline
#2 11. 06. 2021 00:09
Re: Algebra Lagrangeova věta
Všetky delitele čísla 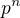 sú jednoduchého tvaru - skús si predstaviť, akého.
sú jednoduchého tvaru - skús si predstaviť, akého.
To budú (na základe spomínaného dôsledku LV) jediné možné rády prvkov grupy G.
Všetky prvky grupy G nemôžu mať rád 1 (prečo?), takže musí existovať nejaký prvok rádu väčšieho ako 1.
Ak vytvoríš cyklickú grupu generovanú týmto prvkom (tá bude podgrupou grupy G), nevedel by si v nej nájsť podgrupu rádu p?
Offline
#4 11. 06. 2021 20:51
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: Algebra Lagrangeova věta
↑ R4d1m3k:
Ahoj, jaký bude řád prvku, který generuje alespoň dvouprvkovou cyklickou grupu?
"Máte úhel beta." "No to nemám."
Offline
#5 11. 06. 2021 20:56
Re: Algebra Lagrangeova věta
↑ check_drummer:
podle toho jak to chápu tak by měl mít řád 2 pro dvouprvkovou grupu
Offline
#6 11. 06. 2021 21:08 Příspěvek uživatele R4d1m3k byl skryt uživatelem R4d1m3k.
#7 11. 06. 2021 21:22
Re: Algebra Lagrangeova věta
↑ check_drummer:
možná jsem se chytil....
kdybych dal  a vzal si teda grupu
a vzal si teda grupu  , tak dělitelé jsou 1, 3 a 9
, tak dělitelé jsou 1, 3 a 9
kdybych chtěl vytvořit grupu právě tou trojkou, tak bych dostal grupu s prvky 0, 3, 6 a její řád je teda 3
trefil jsem to?
Offline
#8 12. 06. 2021 00:11
Re: Algebra Lagrangeova věta
R4d1m3k napsal(a):
jakoby chápu že mezi těmi děliteli bude určitě 1 a p, a spousta dalších...
Otázka je, čo rozumieš pod slovom "spousta" :) . Číslo 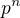 má práve
má práve  deliteľov, a síce
deliteľov, a síce  . Všetky jeho delitele sú tvaru
. Všetky jeho delitele sú tvaru  a teda jedine také hodnoty môže nadobúdať rád každého prvku grupy (o.i. si všimni, že okrem prípadu
a teda jedine také hodnoty môže nadobúdať rád každého prvku grupy (o.i. si všimni, že okrem prípadu 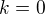 je rád každého prvku deliteľný
je rád každého prvku deliteľný  ).
).
R4d1m3k napsal(a):
trefil jsem to?
V podstate si trafil záverečnú myšlienku.
Ak by pôvodná grupa bola cyklická (ako je napr.  z Tvojho príkladu), ľahko z nej vyberieš podgrupu rádu
z Tvojho príkladu), ľahko z nej vyberieš podgrupu rádu  - tak ako si naznačil.
- tak ako si naznačil.
V cvičení však cyklickosť celej grupy nepredpokladáme. Takže najprv ukážeš existenciu (=vytvoríš) netriviálnu cyklickú podgrupu v grupe G a hľadanú grupu rádu  vyberieš až z nej.
vyberieš až z nej.
Offline
#9 12. 06. 2021 07:43
#10 18. 06. 2021 16:11
Re: Algebra Lagrangeova věta
↑ zdubius:
Teď mě napadá, podle čeho je jisté že v té vytvořené cyklické podgrupe bude vždy podgrupa radi p
Offline
#11 21. 06. 2021 13:01
Re: Algebra Lagrangeova věta
↑ R4d1m3k:
Ospravedlňujem sa za neskoršiu odpoveď, počas víkendu som mal pomerne nahustený program.
K Tvojej otázke: Vo všeobecnosti cyklická grupa generovaná prvkom  má jednoduchú štruktúru - všetky jej prvky sú "mocniny" prvku
má jednoduchú štruktúru - všetky jej prvky sú "mocniny" prvku  (kde mocninou prvku
(kde mocninou prvku  rozumiememe výsledok grupovej operácie prvku
rozumiememe výsledok grupovej operácie prvku  so sebou samým, teda
so sebou samým, teda 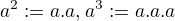 atď.)
atď.)
Pokiaľ rád prvku  je
je  , tak prvky
, tak prvky  sú navzájom rôzne (dôkaz je jednoduchý, ak ste ho nerobili, skús si ho) a teda cyklická grupa generovaná prvom
sú navzájom rôzne (dôkaz je jednoduchý, ak ste ho nerobili, skús si ho) a teda cyklická grupa generovaná prvom  je práve
je práve  Tým pádom aj jej počet prvkov je
Tým pádom aj jej počet prvkov je  .
.
Z predošlej doskusie vieš, že v grupe  musí existovať prvok (označme ho
musí existovať prvok (označme ho  ), ktorého rád je
), ktorého rád je  . Ním generovaná cyklická grupa je teda
. Ním generovaná cyklická grupa je teda 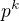 -prvková grupa
-prvková grupa
Ak z tejto grupy vyberieš vhodné prvky (využi, že počet prvkov je deliteľný  , takže vyberaj v rovnakých "rozostupoch"), dostaneš hľadanú
, takže vyberaj v rovnakých "rozostupoch"), dostaneš hľadanú  -prvkovú podgrupu.
-prvkovú podgrupu.
Offline
