Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 11. 2009 14:02
Goniometricka rovnice
Zdravim,
chtel bych se jen zeptat, jak resit presne rovnici:
sin x + cos x + 1 = 0
Ja to resil tak, ze jsem si tu jedna hodil na druhou stranu a tim padem me vyslo, ze sin x + cos x = -1, nacrtnul jsem si grafy funkce sin x a cos x a hledal, kdy se rovnaji -1, to me vyslo, ze v podstate pro cos x je to v pi, sin x je v pi rovna 0, takze vyhovuje a pak sin x ze je -1 v 3/2 pi a v tom samem dobe je cos x rovno 0, takze vysledek je: x1 = pi + 2k pi a x2 = 3/2 pi + 2k pi
Je to spravne a da se tento postup pouzit, pripadne jestli se da pouzit jiny postup, kdy se nepouzivaji grafy ?
Diky moc za radu ;o)
Offline
#3 10. 11. 2009 14:59 — Editoval zdenek1 (10. 11. 2009 15:02)
Re: Goniometricka rovnice
↑ Aleon:Ano, tvůj výsledek je správně.
V tomto případě je lepší postupovat takto:



 nebo
nebo 

 nebo
nebo 

Výhoda je v tom, že právě nemusíš dělat žádnou zkoušku
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 10. 11. 2009 15:12
- marnes

- Příspěvky: 11227
Re: Goniometricka rovnice
↑ zdenek1:Ano, to je lepší metoda, ale musíš mu napsat, čím obě strany obecně dělit, aby tuto úpravu pochopil
Jo. A na začátku vás zdravím.
Offline
#5 10. 11. 2009 15:36
#7 10. 11. 2009 20:31
- marnes

- Příspěvky: 11227
Re: Goniometricka rovnice
↑ zdenek1:
No mě to jasné je, ale dotyčný neví, jak jsi k těm číslům došel. Mě šlo jen o to napsat k tomu, že v těchto typech příkladů se to dělí výrazem  kde a a b jsou ty koeficienty
kde a a b jsou ty koeficienty
Jo. A na začátku vás zdravím.
Offline
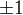 , nebo jeden
, nebo jeden  a druhý
a druhý