Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 11. 2018 19:30
Nekonečná řada
Zdravím, nevím si rady s jedním typem nekonečných řad (vyčíslením nekonečných řad). Jedná se o typ: 
Konkrétně například:  nebo
nebo  .
.
Je mi jasné, že se jedná o  . Mým problémem je, že nemohu přijít na to, jak dané
. Mým problémem je, že nemohu přijít na to, jak dané  najít. Pro
najít. Pro  ve jmenovateli například se později dostávám do dost hnusných čísel, a když se to snažím vyjádřit nějakými násobky apod. tak se mi nedaří najít žádné pravidlo, které by pro čitatel platilo.
ve jmenovateli například se později dostávám do dost hnusných čísel, a když se to snažím vyjádřit nějakými násobky apod. tak se mi nedaří najít žádné pravidlo, které by pro čitatel platilo.
Offline
#2 30. 11. 2018 20:15
Re: Nekonečná řada
↑ Pluhtik:
Ahoj,
Pokud  , potom soucet tve prvni sumy je
, potom soucet tve prvni sumy je 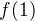 .
.
Pokud si dale oznacis  , pak
, pak  .
.
Sumu  dokazes pro
dokazes pro  secist na
secist na 
Naslednym derivovanim  pak ziskas
pak ziskas  ,
,
a tedy 
Offline
#3 30. 11. 2018 20:21 — Editoval Pavel (30. 11. 2018 20:21)
Re: Nekonečná řada
↑ Pluhtik:
Nechceš-li použít derivace, doporučuji provést tento obrat:
Geometrickou řadu určitě sečíst umíš a  rovnice
rovnice
vyjádřit umíš určitě taky.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 30. 11. 2018 22:53 — Editoval Pluhtik (30. 11. 2018 22:55)
Re: Nekonečná řada
Ani jedno mi po pravdě nedává moc smysl. Derivace spíše používat nebudu, takže reaguji především na Pavla.
S jsi vyjádřil jako násobek sebe sama + součet nějaké jiné řady, jestli jsem to pochopil. Nechápu to a taky se mi to nezdá.
Respektive chápu každý jednotlivý krok, ale čím si pomůžu, když to takhle vyjádřím? Nenapadá mě totiž způsob, jak S pěkně vyjádřit.



To ale nedává smysl. Součet nekonečné řady kladných čísel přece nemůže být záporné číslo.
Offline
#5 30. 11. 2018 23:05
Re: Nekonečná řada
↑ Pluhtik:
Ahoj, tu geometrickou radu v tom Pavlove vyjadreni nejdriv secti ;-)
Offline
#7 30. 11. 2018 23:17 — Editoval laszky (30. 11. 2018 23:18)
Re: Nekonečná řada
↑ Pluhtik:
Soucet geometricke rady s kvocientem  (|q|<1) je
(|q|<1) je  .
.
Takze soucet geometricke rady s kvocientem  je
je 
Offline
#8 30. 11. 2018 23:33 — Editoval Pluhtik (30. 11. 2018 23:43)
Re: Nekonečná řada
Ok, poradil bys mi s tím vyčíslením prosím?
Vychází mi, že:



....
ale nedaří se mi najít  (problém mám zejména s tím čitatelem)
(problém mám zejména s tím čitatelem)
edit. mám to vypočtené, jen si nemyslím, že mi takový výpočet v testu uzná, nejspíš bude chtít vyčíslit limitu. Proto potřebuji znát Sn
Offline
#9 01. 12. 2018 00:05
Re: Nekonečná řada
↑ Pluhtik:
V celém mém výpočtu stačí nahradit v sumě  konečným
konečným  a provést tytéž úpravy:
a provést tytéž úpravy:
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
