Matematické Fórum

Makrofág · 15. 08. 2020 19:09

Ahoj!
Prosímvás, chci ujistit, že má smysl vymyslet lepší definici jednoduché a uzavřené křivky, anebo vysvětlit, proč jsou definice, které zde uvedu, dostačující.

Mám problém s tím, že mám v soustavě souřadnic dány dvě shodné úsečky (tj. rovnají se sobě jakožto množiny bodů), a přesto o jedné z nich můžu říct, že je to jednoduchá křivka (tak by to mělo být) a o druhé říct, že je to uzavřená křivka. To mi vadí. Mám se s tím smířit, anebo tenhle problém volá po změně?

Příběh se má takhle...
Nechť jsou dána dvě různá reálná čísla: 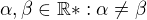$\alpha, \beta \in \mathbb{R*} : \alpha \ne \beta$ . Pak je dán interval: $I=\langle \alpha ; \beta \rangle$ . Dále, nechť jsou dány dvě spojité funkce $f, g$ .
Pak rovinná křivka je $\bigcup_{x \in I}^{}\{[f(x); g(x)]\}$ .

Definoval jsem teď křivku obecně jakoukoliv. Teď definuju křivku jednoduchou a uzavřenou, abych to tady pak strašně rozbalil...

Mějme na křivce $k$ dva body $A, B: A = [f(\alpha); g(\alpha)], B = [f(\beta); g(\beta)]$ .
Pak pokud:
a) $A \ne B$ : $k$ je jednoduchá křivka
b) 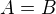$A = B$ : $k$ je uzavřená křivka .

Tak a teď definuju úsečku jakožto jednoduchou křivku: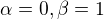
$\alpha = 0, \beta = 1$
$I = \langle 0; 1\rangle$
$f(x) = x$
$g(x) = x$
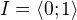
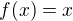
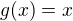
úsečka $l_1$ = $\bigcup_{x \in I}^{}\{[x; x]\}$

Prostě vznikne úsečka s krajními body $[0; 0]$ a $[1; 1]$ .

Nó a teď chci definovat tu samou úsečku jako uzavřenou křivku: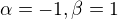
$\alpha = -1, \beta = 1$
$I = \langle -1; 1 \rangle$
$f(x) = |x|$
$g(x) = |x|$
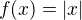
úsečka $l_2$ = $\bigcup_{x \in I}^{}\{[|x|; |x|]\}$

Takže: $l_1 = l_2$ , a přesto $l_1$ je křivka jednoduchá a $l_2$ je křivka uzavřená.

Proč mi to vadí? Protože jsem si o uzavřených křivkách myslel, že dělí rovinu alespoň na dvě disjunktní části. Jenže vidím, že to tak obecně není. Chci v tom mít prostě jasno. Díky, že jste dočetli až sem.

Eratosthenes · 24. 09. 2021 08:58

↑ Makrofág:

>> a) [mathjax]A \ne B[/mathjax] : [mathjax]k[/mathjax] je jednoduchá křivka

To určitě ne

[mathjax]f(x) = \sin 5x; g(x) =\cos 4x[/mathjax]

[mathjax]\alpha = 0; \beta =2\pi[/mathjax]

Aby křivka dělila rovinu na dvě disjunktní množiny, musí být uzavřená a jednoduchá. Ani jedno nemáš definováno dobře. A obávám se, že motáš dohromady křivku a její parametrizaci. To jsou dvě rozdílné věci.

Richard Tuček · 25. 09. 2021 18:47

První křivka (jednoduchá) představuje úsečku z bodu [0;0] do bodu [1;1]
Druhá křivka představuje úsečku z bodu [1;1] do bodu [0;0] a zpět.
Po jedné úsečce jedu dvakrát. Proto vypadají navenek stejně.

MichalAld · 27. 09. 2021 00:08

Mě zas třeba na škole vrtalo hlavou - že ve 3D prostoru nelze vyjádřit přímku jednou rovnicí - tak jako ve 2D - ax + by + c = 0.

Ale rovnice tvaru [mathjax]x^2 + y^2 = 0[/mathjax] je vlastně přímka (osa z). A vhodným posunutím a natočením můžeme takto v principu vyjádřit jakoukoliv přímku...aspoň si to myslím...

Stýv · 27. 09. 2021 00:29

↑ MichalAld: Nejde to jednou linearni rovnici. Nelinarni rovnici je to trivialni.

Matematické Fórum

#1 15. 08. 2020 19:09

Hledání lepší definice rovinné křivky

#2 24. 09. 2021 08:58

Re: Hledání lepší definice rovinné křivky

#3 25. 09. 2021 18:47

Re: Hledání lepší definice rovinné křivky

#4 27. 09. 2021 00:08

Re: Hledání lepší definice rovinné křivky

#5 27. 09. 2021 00:29

Re: Hledání lepší definice rovinné křivky

Zápatí