Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 02. 2012 11:52
Výpočet poločasu rozpadu - posloupnost
Zdravím, mám úkol do školy odvodit vzorec pro výpočet poločasu rozpadu:
Hmotnost izotopu radia je 133 g. Jeho poločas rozpadu je 2,7minut. Určete kolik g zbyde z původního množství daného izotopu Ra za 19 minut. Na první pohled to je jednoduchý a asi i je, vypočítal jsem rozpadovou konstantu λ = ln2/T.
Tedy ln2/2,7 a pak dosadit do vzorce N=N0*exp(λ-t). Jenže musíme odvodit vzorec pomocí posloupnosti a to si ze střední školy už moc nepamatuji a nevím jak se to dá odvodit... Aby to mohlo vyjít dělitelné. Budu rád za nápady. Díky moc :-)
Offline
#2 23. 02. 2012 12:49
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Výpočet poločasu rozpadu - posloupnost
Ahoj,
jedná se o obyčejnou geometrickou posloupnost, stačí napsat "poločas rozpadu" do magického políčka hledat a určitě ti to pomůže :-)
Např:
Poločas rozpadu-GP
Offline
#3 23. 02. 2012 14:03 — Editoval Rumburak (23. 02. 2012 14:39)
Re: Výpočet poločasu rozpadu - posloupnost
Zdravím také. Soudím, že co se má odvodit, není vzorec pro výpočet poločasu rozpadu, ale vzorec N=N0*exp(-λt).
Nechť 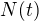 je množství sledované látky v okamžiku
je množství sledované látky v okamžiku 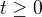 . Je-li poločas jejího rozpadu
. Je-li poločas jejího rozpadu 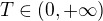 , znamená to, že
, znamená to, že
pro libovolné 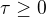 platí
platí 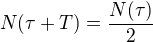 , obecněji
, obecněji  ,
,
jak snadno dokážeme indukcí.
Odhadněme hodnotu 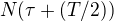 . Podle předešlého musí být
. Podle předešlého musí být 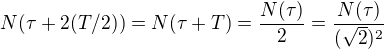
a proto není obtížné přijmout předpokled, že 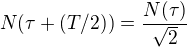 a ještě ho zobecnit na
a ještě ho zobecnit na 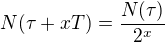
pro obecné 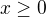 (nejen pro x = n = 0, 1, 2, ... nebo x = 1/2) . Položíme-li zde
(nejen pro x = n = 0, 1, 2, ... nebo x = 1/2) . Položíme-li zde  , máme
, máme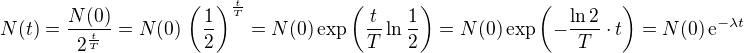 ,
,
jestliže 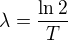 . Je to ono ?
. Je to ono ?
Offline
#5 23. 02. 2012 16:10
Re: Výpočet poločasu rozpadu - posloupnost
Aha. V tom případě se domnívám, že není dohromady co odvozovat. Poločas rozpadu je 2,7minut, zajímá nás, co zbyde za 19 minut.
Offline
#8 09. 06. 2022 23:10
Re: Výpočet poločasu rozpadu - posloupnost
↑ CUllblade:
Polčas rozpadu je doba, za ktorú sa rozpadne polovica sledovaného množstva.
Po uplynutí 1 polčasu rozpadu sa rozpadne 1/2 množstva, a teda zostáva ešte polovica.
Po uplynutí ďalšieho polčasu rozpadu sa rozpadne polovica zo zostávajúceho množstva, čo je polovica z polovice, teda 1/4. Celkovo sa za dva polčasy rozpadu rozpadne 1/2+1/4=3/4 množstva prvku.
Po uplynutí ďalšieho polčasu rozpadu sa ropadne polovica zo zostávajúceho množstva, teda polovica zo štvrtiny, čiže 1/8. Celkovo je už rozpadnutých 1/2+1/4+1/8=7/8 množstva.
Čas, za ktorý sa rozpadne 7/8 pôvodného množstva prvku, teda zodpovedá 3 polčasom rozpadu.
Offline
#9 10. 06. 2022 10:45
- misaH
- Příspěvky: 13467
Re: Výpočet poločasu rozpadu - posloupnost
↑ CUllblade:
Ahoj.
Druhý raz si založ vlastnú tému, ináč vznikajú pri odpovediach zmätky.
Offline
 mi zakázali a měl jsem na to přijít právě pomocí té posloupnosti, oběma moc děkuju za odpověď. Asi jdu dostudovat posloupnosti :-D
mi zakázali a měl jsem na to přijít právě pomocí té posloupnosti, oběma moc děkuju za odpověď. Asi jdu dostudovat posloupnosti :-D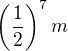 , kde m je počáteční množství. Přesná hodnota zůstatku po 19-ti min. by samozřejmě byla
, kde m je počáteční množství. Přesná hodnota zůstatku po 19-ti min. by samozřejmě byla 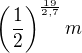 .
. 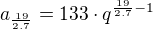 a nevzcházelo to ... díky moc Messieu Rumburak
a nevzcházelo to ... díky moc Messieu Rumburak