Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Izomorfismus struktury a struktury k ní opačné (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 04. 2012 18:49
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Izomorfismus struktury a struktury k ní opačné
Ahoj,
napadl mě tento problém. Zatím jsem nepřemýšlel nad tím, zda a jaké má řešení:
Nechť X:=(A,f) je algebra s jednou (binární) operací f, která není komutativní. Definujme algebru Y:=(A,g), kde g(x,y):=f(y,x). Ptejme se, zda X a Y mohou být izomorfní a za jakých předpokladů toto nastane. Zkoumejme i speciální případ, kdy X,Y jsou grupy.
Sice to není klasická úloha tvaru "najdi / dokaž X", ale bylo by dle mého zajímavé tento problém zkoumat. Možná jsou podmínky dány moc volně, takže "rozumnou" charakteristiku nebude možné najít, možná v případě grup ano.
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) check_drummer)
#2 24. 04. 2012 19:46
Re: Izomorfismus struktury a struktury k ní opačné
Ahoj ↑ check_drummer:,
Prve myslienky:
ja by som na tvojom mieste skusil nejaky iny zapis pre tvoje binarne operacie.
Klasicky sa pise
f(x,y)=z
ako
x*y=z
ale mozme pisat napriklad ako
y
x = z
Morfismy dvoch binarnych operacii pre charakteristicke operacie sa daju naivne vidiet ak mozme pre kazdu z nich najst totozne zapisy.
Na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 24. 04. 2012 20:12 — Editoval Andrejka3 (24. 04. 2012 21:40)
Re: Izomorfismus struktury a struktury k ní opačné
↑ check_drummer:
Ahoj,
zatím jen něco, v noci asi doplním.
Ve sbírce (citace) je příklad:
Ať  grupa a
grupa a  . Platí
. Platí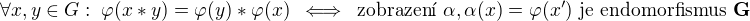 .
.
Myslím, že se najde nějaká souvislost a analogie. Chci navíc, aby  byl bijektivní. Uvidím. Zatím, ahoj.
byl bijektivní. Uvidím. Zatím, ahoj.
edit nevim proc latex failed
edit: Srozumitelnější formulace.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 24. 04. 2012 21:06
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Izomorfismus struktury a struktury k ní opačné
↑ vanok:
Ahoj, pomocí klasického funkčního zápisu mi přišla definice g jasnější - klasický zápis x*y := y.x by možná nebyl tak zřejmý. Ale je to detail.
"Máte úhel beta." "No to nemám."
Offline
#5 24. 04. 2012 21:09 — Editoval check_drummer (24. 04. 2012 21:14)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Izomorfismus struktury a struktury k ní opačné
↑ Andrejka3:
Ahoj, dovoluji si zatím jen upravit výraz, abych viděl celé znění toho tvrzení (místo varpsi píšu varphi)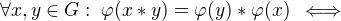
Není mi jasné, jak je na levé straně implikace kvantifikováno  - asi také existenčním kvantifikátorem, že?
- asi také existenčním kvantifikátorem, že?
Asi bude nutné to Tvé tvrzení vhodně zeditovat, aby bylo zřejmé, které funkce je která ( vs.
vs.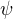 )
)
"Máte úhel beta." "No to nemám."
Offline
#6 24. 04. 2012 21:40 — Editoval Andrejka3 (24. 04. 2012 23:05)
Re: Izomorfismus struktury a struktury k ní opačné
↑ check_drummer:
Editovala jsem to původní znění na srozumitelnější.
Edit, řešení pro grupy: Mějme 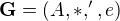 ,
,  grupy
grupy
Je 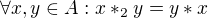 , odkud
, odkud 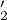 je totéž co
je totéž co  .
.
Buď  automorfismus
automorfismus  . Pak
. Pak  je bijekce na
je bijekce na  a platí
a platí .
.
Tedy,  je isomorfismus
je isomorfismus  .
.
Edit: Vážený kolega constr posílá Odkaz, který je asi to, na co se ptáš. Doufám, že se nebude zlobit, že to zde píši.
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 26. 04. 2012 21:30
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Izomorfismus struktury a struktury k ní opačné
↑ Andrejka3:
Děkuji. Jsem rád, že to nebyl úplný nesmysl, ale že, jak vidím, se tímto pojmem někdo již zabýval. U grup tedy opravdu stačí využít vlastnost existence inverzního prvku, to je pěkné.
"Máte úhel beta." "No to nemám."
Offline
#8 30. 04. 2012 20:35
Re: Izomorfismus struktury a struktury k ní opačné
↑ check_drummer:,
Mala otazka: ako to je z vektorovym priestorom na lavo a v.p. na pravo?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 30. 04. 2012 21:56
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Izomorfismus struktury a struktury k ní opačné
↑ vanok:
Ahoj, co máš prosím na mysli pod "na levo" a "na pravo"? Děkuji.
"Máte úhel beta." "No to nemám."
Offline
#10 30. 04. 2012 23:05
Re: Izomorfismus struktury a struktury k ní opačné
↑ check_drummer:
podobne ako tu
http://en.wikipedia.org/wiki/Module_%28mathematics%29
ide o v.p na nekomutativnych telasach.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Izomorfismus struktury a struktury k ní opačné (TOTO TÉMA JE VYŘEŠENÉ)
