Matematické Fórum

MonikaP · 16. 06. 2012 12:07

Dobrý den, chtěla bych poprosit o radu se dvěma příklady.

1. Kouli je opsán rotační kužel, jehož výška se rovná šestinásobku poloměru koule r=6cm. V jakém poměru jsou povrchy obou těles?

2. Určete délky hran kvádru vepsaného do koule o poloměru r=7cm, jestliže poměr plošných obsahů jeho stěn je 1:2:3.

Předem děkuji za jakoukoli pomoc. Zkoušela jsem počítat a měla jsem v tom nějaké nejasnosti a výpočty mi nevycházeli.

Miky4 · 16. 06. 2012 12:12 — Editoval Miky4 (16. 06. 2012 12:12)

↑ MonikaP:
Dobrý den, napiš, jak jsi to zkoušela počítat, jaké si měla nejasnosti a co ti (ne)vycházelo.

MonikaP · 16. 06. 2012 12:18

V prvním případě znám sice výšku kužele, ale jen z toho nemůžu vypočítat povrch. Vím, že počítám jen poměr, ale nevím jak se k tomu poměru dohrabat.
A v druhém případě znám tělesovou úhlopříčku kvádru, ale nevím, jak vypočítat ty hrany jen pomocí poměrů obsahů.

jelena · 16. 06. 2012 19:59

↑ MonikaP:

Zdravím,

je lepší dávat do tématu jen jednu úlohu a rovnou napsat svůj postup - pravidla.

1) pokud zakreslíš řez kuželu, máš rovnoramenný trojúhelník, do kterého je vepsána kružnice. Zakreslí příčku rovnoběžně základně trojúhelníku a procházející "horním bodem kružnice". Špíška je trojúhelník, který je podobný trojúhelníku v řezu. Jeho výška je 4 poloměry kružnice. je jasné proč?

2) můžeš označit ab:bc:ac=1:2:3=x a odsud po dvojicích pokračovat s vyjádřením jednotlivých stran a, b, c.
Z faktu, že kvádr je vepsán do koule máš vyjádření tělesové uhlopříčky (průměr koule) přes a, b, c.
Měla bys mít rovnici s jednou neznámou x.

Podaří se pokračovat? Děkuji.

MonikaP

Omlouvám se, zaregistrovala jsem se nedávno a pravidla jsem ještě nepřečetla. Už jsem poučená.

Druhý příklad jsem vypočítala už bez problému. Moc děkuji za pomoc. A v prvním příkladě jsem už měla nakreslený trojúhelník s vepsanou kružnicí, chápu, že si jsou ty dva trojúhelníky podobné, chápu, že výška špičky jsou 4 poloměry kružnice, ale pořád nechápu, jak se mám dostat k tomu poměru.

jelena · 17. 06. 2012 15:38

↑ MonikaP:

to je v pořádku :-)

Povrch koule máme vyjádřený přes r koule. Potřebujeme vyjádřit přes r také povrch kuželu.

Pokud v trojúhelníku v řezu sestrojím kolmici ze středu kružnice na rameno trojúhelníku (patu kolmice označím T), potom v pravoúhlém trojúhelníku SVT máme délku |ST|=r, |SV|=5r.

Můžeme tedy vyjádřit sin(TVS)=r/5r, odsud můžeme odvodit další goniometrické funkce úhlu (nebudeme počítat, ale odvozovat). Druhá možnost je určení délky TV přes Pythagorovu větu.

V trojúhelníku AXV (AX je polovina strany AB základny řezu, zároveň je to poloměr podstavy kuželu) XV výška kuželu, proto |XV|=6r).

Zde využijeme podobnost trojúhelníku AXV a STV pro určení zbývajících rozměrů, co potřebujeme (poloměr podstavy kuželu a délku boční strany).

kolop · 18. 12. 2015 20:58

kouli je opsán rotační kužel,jehož výška se rovná šestinásobku poloměru koule r=6cm.V jakém poměru jsou povrchy obou těles?
potřeboval bych to prosím vypočítat probíráme to ve stereometrii nějakým postupem abych to pochopil matematika mi moc nejde děkuji

jelena · 18. 12. 2015 21:35

↑ kolop:

Zdravím,

tato úloha je již v tématu naznačena, ale jen schematicky

1) pokud zakreslíš řez kuželu, máš rovnoramenný trojúhelník, do kterého je vepsána kružnice. Zakreslí příčku rovnoběžně základně trojúhelníku a procházející "horním bodem kružnice". Špíčka je trojúhelník, který je podobný trojúhelníku v řezu. Jeho výška je 4 poloměry kružnice. je jasné proč?

Povrch koule máme vyjádřený přes r koule. Potřebujeme vyjádřit přes r také povrch kuželu.

Pokud v trojúhelníku v řezu sestrojím kolmici ze středu kružnice na rameno trojúhelníku (patu kolmice označím T), potom v pravoúhlém trojúhelníku SVT máme délku |ST|=r, |SV|=5r.

Můžeme tedy vyjádřit sin(TVS)=r/5r, odsud můžeme odvodit další goniometrické funkce úhlu (nebudeme počítat, ale odvozovat). Druhá možnost je určení délky TV přes Pythagorovu větu.

V trojúhelníku AXV (AX je polovina strany AB základny řezu, zároveň je to poloměr podstavy kuželu) XV výška kuželu, proto |XV|=6r).

Zde využijeme podobnost trojúhelníku AXV a STV pro určení zbývajících rozměrů, co potřebujeme (poloměr podstavy kuželu a délku boční strany).

Obrázek si vypůjčím od kolegy Cheopa z tématu - viz Obrázek Pro řešení využíváme trojúhelník s oranžovou základnou (jeho výška je 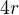$4r$ ) a trojúhelník s modrou základnou. Trojúhelníky jsou si podobny. Nakresli si obrázek a zkus, prosím, odvodit vztahy, jak je popsáno. Ozvi se, jak to šlo. Děkuji.

kolop · 18. 12. 2015 21:59

dobrý den moc se omlouvám ale nemám ani tušení jak to vypočítat probíráme ted stereometrii a nemám ani ponětí jak na to nešlo by to prosím vysvětlit jako pro blbce :)

jelena · 18. 12. 2015 22:59 — Editoval jelena (19. 12. 2015 09:26)

↑ kolop:

to je trošku problém - úloha není úplně snadná, pokud se v látce moc neorientuješ. Máš propočteno více úloh? Jelikož potřebuješ:

a) mít představu obrázku pro zadanou situaci "kouli je opsán kužel" v prostoru,
b)"přetvořit" tento obrázek do roviny řezu (na obrázku vidíme rovnoramenný trojúhelník, který vznikne řezem kuželu rovinou kolmou podstavě a procházející hlavní osou kuželu. Do trojúhelníku je vepsán kruh, který vznikne v řezu koule),
c) vyznačit zadané údaje,
d) úloha požaduje poměr povrchů, proto vypsat vzorce pro povrchy koule a kuželu,
e) vyznačit, co ve vzorcích víme a co je třeba odvodit ze zadání.

Tak dojdeš k závěru, že vzorec pro objem koule můžeš použit tak, jak je z tabulek. Ale ve vzorci pro povrch kuželu musíš vyjadřovat jak výšku, tak poloměr podstavy, tak boční stěnu přes poloměr koule.

Více - to už bych musela vyřešit úlohu celou, tak to není správné - váš učitel musí vědět, co dokážete samostatně, popřípadě s nějakou nápovědou. Ať se podaří s úlohou pokročit.

Edit: úloha požaduje poměr povrchů - opraveno.

kolop · 18. 12. 2015 23:06

opravdu by ste to nemohla vypočítat moc prosím :( byl bych vám moc vděčný :)

jelena · 18. 12. 2015 23:56 — Editoval jelena (19. 12. 2015 09:26)

↑ kolop: tak alespoň napůl :-) Ty uděláš obrázek, vyznačíš všechno, co je zadáno a napíšeš poměr povrchů. Já odvodím poloměr podstavy kuželu. Ale až zítra. Vděčni si budeme.

kolop · 19. 12. 2015 00:20

Dobře děkuji :)

jelena · 19. 12. 2015 09:28

↑ kolop: dobře, jen si ještě, prosím všimni mého editu v příspěvcích - úloha požaduje poměr povrchů (ne objemů, jak jsem psala), ale postup a dělba práce jsou stejné :-), jen vzorce budou pro povrch, ne pro objem.

kolop · 30. 12. 2015 01:21

Co dosadim do Pythagorovy věty znám jenom R=6cm a výšku sestinasobek poloměru r=6cm takže v=36cm ale to mi pak nevychází? [/hide]

misaH · 30. 12. 2015 02:26 — Editoval misaH (30. 12. 2015 02:27)

↑ kolop:

Poriadne si prečítaj odporúčaný postup.

Máš obrázok podľa návodu?

(Existuje ale aj postup bez sinusu a podobnosti...)

kolop · 30. 12. 2015 13:15

Už vím jak na to ale potřeboval bych vědět jak zjistím poloměr podstavy kužele když znám akorát výšku a ta je 36cm a že kouli je opsan rotační kužel a poloměr té Koule je 6cm
Ale jak zjistím poloměr podstavy kužele? Děkuji

misaH · 30. 12. 2015 14:02 — Editoval misaH (30. 12. 2015 14:04)

↑ kolop:

Veď ti to jelena popisuje.

Ja by som použila postup cez obsah trojuholníkov.

kolop · 30. 12. 2015 15:56

Už myslím že my to vyšlo jsou poměry 4:9 povrchy 452.4cm a 993 cm?
Koule a kužel

jelena · 31. 12. 2015 00:38

↑ kolop:

Zdravím, číselně jsem dopočetla, abych porovnala s Tvým výsledkem (ale místo 993 mám cca 1017, nejspíš jsi "více" zaokrouhloval), lepší však zapisovat konečné vyjádření povrchů tak, jak vyšlo z odvození.
Povrch koule je vzorec z tabulek 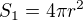$S_1=4\pi r^2$ , povrch kuželu mi vyšel po úpravě $S_2=9\pi r^2$ , poměr povrchů nezávisí na konkrétní hodnotě $r$ koule. Pokud ještě potřebuješ kontrolu, tak rozepiš, prosím, odvození pro rozměry kuželu.

kolop · 07. 01. 2016 09:35

Já sem r kužele vypočítal přes osu X y ale to mi neuznala jak vypocitam r kužele znamli jen výšku 36cm? Děkuji

misaH · 07. 01. 2016 10:48 — Editoval misaH (07. 01. 2016 11:13)

↑ kolop:

No - rátala by som cez obsahy.

Označíme polomer kužeľa R.

Potom platí, že obsah polovice prierezového trojuholníka je

$\frac {R\cdot 36}{2}$

Ten istý trojuholník má obsah $\frac {s\cdot 6}{2}+\frac {R\cdot 6}{2}$ (spojíš stred kružnice s 1 vrcholom základne)

Z rovnosti obsahov $s=5R$ .

Z Pytagorovej vety 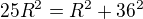$25R^2=R^2+36^2$

Preto 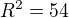$R^2=54$

Potom už hľadaný pomer povrchov (guľa:kužeľ)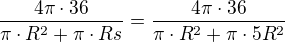

$\frac {4\pi\cdot 36}{\pi\cdot R^2+\pi\cdot Rs}=\frac {4\pi\cdot 36}{\pi\cdot R^2+\pi\cdot 5R^2}$

Teda: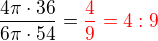

$\frac {4\pi\cdot 36}{6\pi\cdot 54}=\color {red}\frac49=4:9$

Ale dá sa postupovať aj ináč.

Pani moderátorka ako vždy iste pozná lepší postup...

jelena · 07. 01. 2016 12:09

Zdravím,

↑ kolop: napiš, prosím, podrobně celý Tvůj postup, ať je jasné, proč paní učitelka neuznala a co by šlo opravit, abys úlohu úspěšně dokončil. Děkuji.

kolop · 07. 01. 2016 17:01

Narysoval sem osu X y označil na ní výšku Teda 36cm udělal sem kružnici o poloměru 6cm a spojil vrchol s hranou kružnice a na ose X mi vyšlo 7,2 poté sem podle Pythagorovy věty dopocital s což vyšlo 36,71 cm
A pak už jen dosadil koule S=4*pí*r
Kužel S pí*r (r+s) a poměr jsem měl už jen podle výsledků protože nevím jak poměr vypočítat hledal sem na internetu ale nic sem nenašel

Matematické Fórum

#1 16. 06. 2012 12:07

Povrchy těles

#2 16. 06. 2012 12:12 — Editoval Miky4 (16. 06. 2012 12:12)

Re: Povrchy těles

#3 16. 06. 2012 12:18

Re: Povrchy těles

#4 16. 06. 2012 19:59

Re: Povrchy těles

#5 17. 06. 2012 14:39 — Editoval MonikaP (17. 06. 2012 14:47)

Re: Povrchy těles

#6 17. 06. 2012 15:38

Re: Povrchy těles

#7 18. 12. 2015 20:57 Příspěvek uživatele kolop byl skryt uživatelem kolop.

#8 18. 12. 2015 20:58

Re: Povrchy těles

#9 18. 12. 2015 21:35

Re: Povrchy těles

#10 18. 12. 2015 21:59

Re: Povrchy těles

#11 18. 12. 2015 22:59 — Editoval jelena (19. 12. 2015 09:26)

Re: Povrchy těles

#12 18. 12. 2015 23:06

Re: Povrchy těles

#13 18. 12. 2015 23:56 — Editoval jelena (19. 12. 2015 09:26)

Re: Povrchy těles

#14 19. 12. 2015 00:20

Re: Povrchy těles

#15 19. 12. 2015 09:28

Re: Povrchy těles

#16 30. 12. 2015 01:21

Re: Povrchy těles

#17 30. 12. 2015 02:26 — Editoval misaH (30. 12. 2015 02:27)

Re: Povrchy těles

#18 30. 12. 2015 13:15

Re: Povrchy těles

#19 30. 12. 2015 14:02 — Editoval misaH (30. 12. 2015 14:04)

Re: Povrchy těles

#20 30. 12. 2015 15:56

Re: Povrchy těles

#21 31. 12. 2015 00:38

Re: Povrchy těles

#22 07. 01. 2016 09:35

Re: Povrchy těles

#23 07. 01. 2016 10:48 — Editoval misaH (07. 01. 2016 11:13)

Re: Povrchy těles

#24 07. 01. 2016 12:09

Re: Povrchy těles

#25 07. 01. 2016 17:01

Re: Povrchy těles

Zápatí