Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 12. 2012 18:34
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Kontrola integrálu
Ahoj,
prosím o kontrolu výpočtu integrálu.![kopírovat do textarea $\int_{}^{}\frac{1}{1+sinx}dx=[sinx=\frac{2t}{1+t^{2}};dx=\frac{2}{1+t^{2}}dt]=\int_{}^{}\frac{2dt}{(t+1)^{2}}=\\=2\int_{}^{}(t+1)^{-2}dt=[t+1=u;dt=du]=2\int_{}^{}u^{-2}du=2\frac{u^{-1}}{-1}=\frac{-2}{t+1}=\frac{-2}{tg\frac{x}{2}+1}+C$](/mathtex/86/8674c3eec76ad1d214818dd0ccafaabe.gif)
Díky, Lenka
Offline
#2 09. 12. 2012 20:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kontrola integrálu
Zdravím,
pro kontrolu můžeš použit MAW. Mně se zdá pohodlnější pro výpočet úprava:
a podělit člen po členu - první je tabulkový, druhý substituce cos(x)=t. Případně se ozví, pokud ještě bude potřeba. Děkuji.
Offline
#3 09. 12. 2012 20:43
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Kontrola integrálu
↑ jelena:
Si nejsem úplně jistá, jak to myslíš podělit ... můžeš mi napovědět? Díky
Offline
#4 09. 12. 2012 21:12
Re: Kontrola integrálu
↑ Dale.Lenka:
asi bylo míněno toto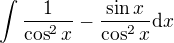
Radim, tedy jsem.
Dobrá rada je drahá, ta moje je zdarma.
Offline
#5 09. 12. 2012 21:14
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Kontrola integrálu
↑ rleg:
Díky, před chvilkou mi to taky došlo :-)
Offline
#7 09. 12. 2012 22:43
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kontrola integrálu
↑ Bati:
Zdravím, doplň to ještě prosím, až budeš mít čas (univerzální goniometrická substituce také má omezení na def. obor - je tak?)
Jinak mne potěšilo, že když jsem se dívala do historie MAW, tak tento integrál se zadával v ukrajinské jazykové verzi, dobře, že se používá.
Offline
#8 09. 12. 2012 23:31
Re: Kontrola integrálu
↑ jelena:
Integrál  můžeme chtít spočítat např. na intervalu
můžeme chtít spočítat např. na intervalu 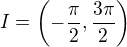 , na větším intervalu už by integrovaná funkce nebyla definovaná.
, na větším intervalu už by integrovaná funkce nebyla definovaná.
Pokud funkci rozšíříme na  , tak tato nová funkce není definovaná v bodě
, tak tato nová funkce není definovaná v bodě 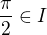 . Můžeme ale integrovat na intervalech
. Můžeme ale integrovat na intervalech 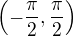 a
a  zvlášť a dostat tak funkce
zvlášť a dostat tak funkce 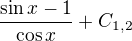 . Protože integrovaná funkce byla spojitá na
. Protože integrovaná funkce byla spojitá na  , existuje k ní primitivní funkce na
, existuje k ní primitivní funkce na  , kterou můžeme najít vhodnou volbou konstant
, kterou můžeme najít vhodnou volbou konstant 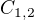 . V tomto případě je to triviální, protože
. V tomto případě je to triviální, protože  , a tedy
, a tedy  , ale je snad jasné, že obecně by to tak být nemuselo a to je důvod, proč jsem na to upozornil - je třeba vědět, že takový problém může nastat. Např. zde:
, ale je snad jasné, že obecně by to tak být nemuselo a to je důvod, proč jsem na to upozornil - je třeba vědět, že takový problém může nastat. Např. zde:  už by to slepování nebylo tak triviální.
už by to slepování nebylo tak triviální.
Samozřejmě, že pokud se v tomto příkladě použije substituce  , tak platí to samé, jen problémový bod bude
, tak platí to samé, jen problémový bod bude  .
.
Offline
#9 10. 12. 2012 10:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kontrola integrálu
↑ Bati:
děkuji za podrobné vysvětlení. Už opakovaně při výpočtu neurčitého integrálu narážím na neuvážení okolností použití substituce nebo úprav - zde také. Tak to beru, že univerzální substituce se zavedou i včetně podmínek (obdobně i algebraické úpravy - samozřejmě, že jen za použití platnosti úprav), ale už ne s dopadem na výsledek. Toho bych si všimla u určitého integrálu např. při změně mezí.
Děkuji velice, že přispíváte i cestou korekce příspěvků - chybí takový odborný dohled (aby to zde neupadalo).
Offline
