Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definice Eulerova čísla (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 07. 2013 14:53
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Definice Eulerova čísla
Ahoj,
existuje více definic Eulerova čísla, např.: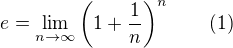

e je jediné číslo takové, že platí 
A teď k otázce: Jak se ukáže, že existuje číslo, vyhovující (3)? Jak se ukáže, že existuje právě jedno? A jak se ukáže, že všechny tyto definice jsou ekvivalentní? Tím myslím, že všechny nám zadávají stejné e?
Děkuji, Honza
PS: dále by se dalo pracovat např. s tím, že e je jediné číslo takové, že 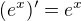 apod... Byla by to také funkční definice? Jak souvisí s (3)?
apod... Byla by to také funkční definice? Jak souvisí s (3)?
Offline
- (téma jako vyřešené označil(a) Hanis)
#3 22. 07. 2013 15:39 — Editoval Rumburak (22. 07. 2013 16:17)
Re: Definice Eulerova čísla
↑ Hanis:
Ahoj.
Také např. rovnicí  a mnoha dalšími způsoby.
a mnoha dalšími způsoby.
Ekvivalence dvou takových způsobů samozřejmě má důkaz spadající do matematické analýzy.
Kdyžtak napiš, který takový důkaz by Tě zajímal, a můžeme se zde na to podívat.
Ještě sem za chvíli dodám jeden link, až ho najdu.
Slíbený link
Zdravím též kolegu Vanka (v naději, že jeho uživatelské jméno správně skloňuji :-) ) .
Offline
#4 22. 07. 2013 15:43
Re: Definice Eulerova čísla
Ahoj ↑ Hanis:
Rychla poznamka:
Nemalo by to byt, najmensie ( infimum) cislo pre ktore plati (3).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 22. 07. 2013 16:17
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Definice Eulerova čísla
Děkuji za doplnění dalších vlastností čísla e.
↑ Rumburak:
Téma prostuduji v nejbližší době, až budu mít chvíli klidného času, moc děkuji.
↑ vanok:
Cituji z knihy Kapitoly z diskrétní matematiky autorů Jiří Matooušek a Jaroslav Nešetřil, ISBN978-80-246-1411-3, str.90:
...Fakt (3) totiž číslo e charakterizuje, pokud pro nějaké reálné číslo a platí
pro všechna reálná x, potom už a=e...
Mne by zajímal důkaz (jednoznačnosti) existence takového čísla a následně důkaz, že je to e, tj. ekvivalenci s (1) nebo (2). Samozřejmě i v knihách mohou být chyby, nicméně mezi studenty i vyučujícími je tato kniha považována za kvalitní.
Offline
#6 22. 07. 2013 17:27 — Editoval Rumburak (23. 07. 2013 15:26)
Re: Definice Eulerova čísla
↑ Hanis:
Když o tom blíže zauvažujeme, tak ta věta citovaná z knihy je správná.
Důkaz založený na definicích
 ,
, 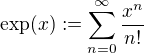 ,
,  je funkce inversní k
je funkce inversní k 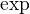 ,
, 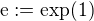
a větách z nich dokazatelných (nevím, jak rychle mi to půjde, dnes mám na to už jen půlhodinu, možná bude nutno dokončit to později):
1) Platí-li pro každé reálné  nerovnost
nerovnost 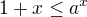 , pak její pravá strana musí mít ve všech zmíněných případech smysl, proto
, pak její pravá strana musí mít ve všech zmíněných případech smysl, proto  .
.
2) Položme  . Ukážeme, že
. Ukážeme, že 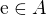 :
:
 .
.
3) Je -li  , ukážeme, že
, ukážeme, že 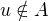 :
:
Položme 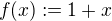 ,
,  , Platí
, Platí 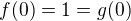 , dále
, dále  , avšak
, avšak  , takže
, takže , odtud
, odtud  . Z těchto srovnání funkcí
. Z těchto srovnání funkcí  plyne:
plyne:
existuje  takové, že pro všechna
takové, že pro všechna  je
je  ,
,
tudíž 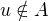 .
.
Celkem jsme dokázali :  .
.
Podobně (i když o něco složitěji) by se dokázalo  , kde
, kde  .
.
Celkem  . Odtud už je ta citovaná věta zřejmá.
. Odtud už je ta citovaná věta zřejmá.
EDIT. Ještě jsem opravil některé překlepy a nepřesnosti.
Offline
#7 22. 07. 2013 17:54
Re: Definice Eulerova čísla
Pozdravujem ↑ Rumburak:,
Ano to je vyborne riesenie, ja som uvazoval v rychlosti len pripad x>0... a pochopitelne pre negativne x, mame riesenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 22. 07. 2013 21:28
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Definice Eulerova čísla
↑ Rumburak:
Moc děkuji za krásné řešení, které je docela snadné - osobně jsem čekal použití věty o supremu/infimu, ale nedokázal jsem to správně zformulovat.
Teď si v rámci cvičení projdu ostatní ekvivalence, kdyby byl nějaký problém, ozvu se.
Offline
#9 22. 07. 2013 22:14
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Definice Eulerova čísla
↑ Rumburak:
Ahoj, nepotřebujeme náhodnou pro odvození hodnoty 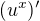 právě dokazovaný tvar čísla e? (Pak bychom využívali to, co chceme dokázat.)
právě dokazovaný tvar čísla e? (Pak bychom využívali to, co chceme dokázat.)
"Máte úhel beta." "No to nemám."
Offline
#11 23. 07. 2013 09:26
Re: Definice Eulerova čísla
↑ check_drummer:
Ahoj.
Podle věty o derivaci složené funkce zde máme
 .
.
Offline
#12 23. 07. 2013 10:39
Re: Definice Eulerova čísla
↑ Rumburak:
Jak správně vystihl ↑ check_drummer:, motáš se v kruhu. Otázka zní, jak definovat e. jestliže k tomu potřebuješ něco takového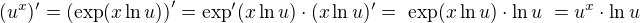
pak musíš definovat funkce  a
a 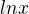 , aniž bys znal číslo e. A to jsem moc zvědav, jak to uděláš :-)
, aniž bys znal číslo e. A to jsem moc zvědav, jak to uděláš :-)
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#13 23. 07. 2013 11:53 — Editoval Rumburak (23. 07. 2013 15:48)
Re: Definice Eulerova čísla
martisek napsal(a):
↑ Rumburak:
Jak správně vystihl ↑ check_drummer:, motáš se v kruhu. Otázka zní, jak definovat e. jestliže k tomu potřebuješ něco takového
pak musíš definovat funkcea
, aniž bys znal číslo e. A to jsem moc zvědav, jak to uděláš :-)
Tak tedy podrobněji:
Za definice zde beru
I.) 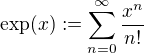 , pokud (prozatím)
, pokud (prozatím)  je reálné
je reálné
(některé vlastnosti této funkce jsou dány teorií řad resp. mocninných řad; pomocí věty o součinu abs. konv. řad dostaneme
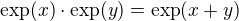 ,
,
odtud plynou vlatnosti této funkce, pokud jde o její průběh, mj. že jde o rostoucí funkci zobrazující 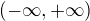 na
na 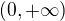 ),
),
II.) 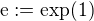 ,
,
III.)  je inversní funkcí k
je inversní funkcí k 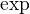
(dle I. speciálně dostáváme  ),
),
IV.)  , pokud
, pokud  ,
,  iracionální
iracionální
(definici mocniny pro  racionální zajišťuje algebra, tato definice je jejím rozšířením, jak lze snadno dokázat;
racionální zajišťuje algebra, tato definice je jejím rozšířením, jak lze snadno dokázat;
speciálně tedy  ).
).
Zatím ten kruh v definicích či v důkazech nevidím :-) .
EDIT: Abychom si rozuměli: já jsem Hanisův výrok (3) nijak nebral za definici čísla  , ale snažil jsem se ukázat,
, ale snažil jsem se ukázat,
že jedině při  tento výrok platí, předpokládaje, že
tento výrok platí, předpokládaje, že  už definováno je a má známé vlastnosti.
už definováno je a má známé vlastnosti.
Offline
#14 23. 07. 2013 12:42
Re: Definice Eulerova čísla
↑ Rumburak:,
Aj velmi znama kniha od W. Rudin-a
http://www.amazon.com/gp/search?index=b … 0070542341
definuje exponencionalnu funkciu ako ty. (historicky, Euler ju definoval ako v (1), a neskor Newton ako v (2), a co da jej predlzenie na complexne cisla....)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 23. 07. 2013 13:57 — Editoval Bati (23. 07. 2013 15:10)
Re: Definice Eulerova čísla
↑ Rumburak:
Souhlasím z Rumburakem, tento postup přes mocninné řady neobsahuje žádný "kruh" a mně osobně přijde nejjednodušší.
Doplním, jak z toho plyne vlastnost (1):
Ještě mě napadlo, jak odvodit vlastnost (3) pomocí hledání extrémů:
Offline
#16 23. 07. 2013 16:33 — Editoval Freedy (23. 07. 2013 16:34)
Re: Definice Eulerova čísla
martisek napsal(a):
↑ Freedy:
Ahoj,
odkud máš
maximum funkce:?
To je totiž nesmysl -je definovaná jenom pro přirozená x.
:D nejsem žádnej zkušenej analytik ani nic podobnýho, s e jsem se (až na zajímavost přirozeného logaritmu při probírání logaritmické funkce) nesetkal. Derivuju si jen ze zajímavosti, chodím do druháku, ale tak zkusím to objasnit, kdyžtak mě opravte:![kopírovat do textarea $f:y=\sqrt[x]{x}=x^{\frac{1}{x}}$](/mathtex/c5/c5872b27bf48c49f94e4aaf073da538e.gif)
hledám maximum této funkce
zderivuju ji: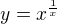

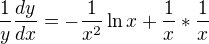
![kopírovat do textarea $\frac{dy}{dx}=y[\frac{1}{x^2}-\frac{\ln x}{x^2}]$](/mathtex/0d/0d3ab38b8281c70e3f2aa6cd1ef8a562.gif)
![kopírovat do textarea $\frac{dy}{dx}=x^{\frac{1}{x}}[\frac{1}{x^2}(1-\ln x)]$](/mathtex/fe/fe01ddd55ad7e35c540f6ae32bc25a2a.gif)
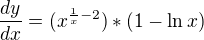
takže:![kopírovat do textarea $\frac{d(\sqrt[x]{x})}{dx}=(x^{\frac{1}{x}-2})*(1-\ln x)$](/mathtex/b2/b2b0c079820d1fd6d3683394411e1b02.gif)
když to položím nule:
vyjde jedno řešení a to je e: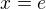
PS: proč pro přirozená x? Stačí ji definovat pro kladná x a je to. A tady to úplně stačí
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#17 23. 07. 2013 17:12 — Editoval Brano (23. 07. 2013 17:13)
Re: Definice Eulerova čísla
↑ Freedy:
samozrejme, ze sa da definovat aj pre ine ako prirodzene cisla ... dokonca ako (relativne pekna) multifunkcia aj pre komplexne cisla - a aj tam sa da vybrat nejaka vetva
ale ked pises "maximum ![kopírovat do textarea $\sqrt[x]x$](/mathtex/1e/1e6bdd800b146f379b165f49f0d736df.gif) " tak by si mal uviest na akej mnozine (t.j. napr. na kladnych cislach) lebo na zapornych ma hlavna vetva aj realnu aj komplexnu zlozku neohranicenu
" tak by si mal uviest na akej mnozine (t.j. napr. na kladnych cislach) lebo na zapornych ma hlavna vetva aj realnu aj komplexnu zlozku neohranicenu
a vlastne  nie je maximum ale bod maxima
nie je maximum ale bod maxima
Offline
#20 23. 07. 2013 18:16
Re: Definice Eulerova čísla
↑ Rumburak:
Za definice zde beru 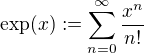
...pak je to OK.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#21 23. 07. 2013 18:23
Re: Definice Eulerova čísla
tak kdyby ti někdo řekl že bod maxima této funkce je e, tak by jsi si ten graf nakreslil a zjistil by jsi, kde má maximum, a potom by si se mu už jen nějakou metodou přibližoval
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#22 23. 07. 2013 18:43 — Editoval martisek (23. 07. 2013 18:56)
Re: Definice Eulerova čísla
↑ Freedy:
Dobrá, tak jinak - jak víš, že (ln x)' = 1/x (když neznáš e)?
To je totiž přesně to, na co upozorňoval ↑ check_drummer:...
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#23 23. 07. 2013 19:11
Re: Definice Eulerova čísla
hm... okay, tak to neni definice... jen říkám že kdyby sis nakreslil graf tehle funkce tak bude mít maximum v e.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#24 24. 07. 2013 00:09
Re: Definice Eulerova čísla
definicia: ![kopírovat do textarea $e:=\text{argmax}_{\{x\in R^+\}}\sqrt[x]x$](/mathtex/48/48846e766efe1b316a64eff5fe735a41.gif) je dokonale jednoznacna
je dokonale jednoznacna
problem moze byt len zistit kolko to je...
a znova ako jednoduchy sa crta standardny postup ktory spominal rumburak
definuje sa 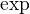 radom
radom 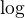 ako inverzna funkcia (ktore v skutocnosi musime mat aby sme mohli vobec definovat
ako inverzna funkcia (ktore v skutocnosi musime mat aby sme mohli vobec definovat ![kopírovat do textarea $\sqrt[x]x$](/mathtex/1e/1e6bdd800b146f379b165f49f0d736df.gif) ) a potom sa lahko dokaze ze
) a potom sa lahko dokaze ze 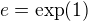
Offline
#25 24. 07. 2013 00:57 — Editoval martisek (24. 07. 2013 01:35)
Re: Definice Eulerova čísla
↑ Brano:
A to já až nebudu mít co dělat, tak si zadefinuju číslo tři. Při konstrukci reálných čísel trojku záměrně vynechám, celou analýzu vybuduji na množině  a neexistenci limit typu
a neexistenci limit typu 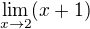 pak vybaven mocným analytickým aparátem vyřeším tímto dodefinováním:
pak vybaven mocným analytickým aparátem vyřeším tímto dodefinováním:
A bude to taky zcela korektní...
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definice Eulerova čísla (TOTO TÉMA JE VYŘEŠENÉ)
![kopírovat do textarea $e=\lim_{n\to\infty }\frac{n}{\sqrt[n]{n}}~~~~~~(4)$](/mathtex/25/25be3bc6d49a929d5b7b7ddbbc836677.gif)
![kopírovat do textarea $e = \lim_{n\to0}\sqrt[n]{1+n}~~~~~~(5)$](/mathtex/a8/a87bfddc5316ba7e1af70078dd53e3d2.gif)
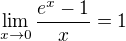 . S použitím této limty, rostoucnosti exp a věty o limitě složené funkce dostáváme, že i
. S použitím této limty, rostoucnosti exp a věty o limitě složené funkce dostáváme, že i 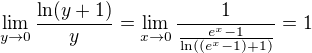 . Teď stačí využít definici obecné mocniny:
. Teď stačí využít definici obecné mocniny: 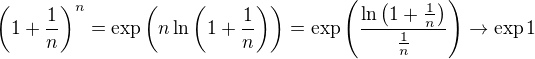 ze spojitosti exp.
ze spojitosti exp.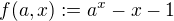 . Chci zjistit, jestli existuje
. Chci zjistit, jestli existuje  , že pro všechna
, že pro všechna 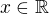 je
je  . Zřejmě musí být
. Zřejmě musí být  , jinak
, jinak  .
.  , takže funkce
, takže funkce  je konvexní pro pevné
je konvexní pro pevné 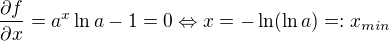 . Definuji funkci
. Definuji funkci 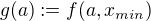 , což je tedy minimální hodnota
, což je tedy minimální hodnota  . Pomocí
. Pomocí  a krajních limit se snadno ukáže, že tato funkce nabývá maxima na intervalu
a krajních limit se snadno ukáže, že tato funkce nabývá maxima na intervalu 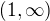 v bodě
v bodě  a hodnota tohoto maxima je 0.
a hodnota tohoto maxima je 0. resp.
resp.  , (tvůj třetí řádek), když ještě nevíš, co je e?
, (tvůj třetí řádek), když ještě nevíš, co je e?