Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 01. 2014 17:24
- lukasstork

- Příspěvky: 57
- Reputace: 0
rovnice s paramtrem
Ahoj potreboval bych pomoci s temihle dvema priklady kde a je realny parametr![kopírovat do textarea $[a/(1+x)-4]/(ax+a)=1-(2/a)$](/mathtex/f7/f790a2fcd597709cc006978f84aebbbb.gif)
![kopírovat do textarea $[(x^{2})/(a+3)]+0,5=x\cdot (a+1)/2a+6$](/mathtex/00/0066593f3dd3a9c59658c6d490945277.gif)
Offline
#2 24. 01. 2014 09:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice s paramtrem
Ještě pozdrav,
první úlohu konzultujeme zde.
2. úloha - je tak? 
Zkontroluj, prosím, zápisy a přidej své návrhy k řešení viz pravidla. Děkuji.
Offline
#3 24. 01. 2014 17:08
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: rovnice s paramtrem
↑ jelena: ahoj ta 6 je taky ve jmenovateli
Offline
#4 24. 01. 2014 18:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice s paramtrem
↑ lukasstork:
no tak to můžeš opravit (klepnutím na zápis ho přeneseš do zprávy a opravíš), vytknout v jmenovateli zlomku napravo číslo 2 a směle vpřed s vlastními návrhy - viz vzorové řešení v 2. tématu.
Offline
#6 24. 01. 2014 19:03
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: rovnice s paramtrem
↑ lukasstork: tu levou stranu bych secet a pak to vsechno vynasobil 2(a+3) a potom nevim
Offline
#7 24. 01. 2014 19:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice s paramtrem
↑ lukasstork:
násobit jmenovatelem můžeš pouze v případě, že jmenovatel není 0. To ještě nemáš ošetřeno.
Tedy začni hned pohledem na zadání a pro které a rovnice nemá smysl - to bude 1. bod do diskuse parametru. Potom tak, jak navrhuješ - všechno převést nalevo, společný jmenovatel, napravo =0 a diskutovat, kdy je zlomek nulový.
Offline
#8 25. 01. 2014 07:05
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: rovnice s paramtrem
↑ jelena: po úpravě mi vyšel diskriminant jako další kvadraticka rovnice 2x^2-x(a+1)+(a+3) je to prosím správně
Offline
#9 25. 01. 2014 08:28
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: rovnice s paramtrem
↑ jelena: a pak nevím co s tím dal
Offline
#10 25. 01. 2014 09:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice s paramtrem
↑ lukasstork:
spíš nám tak vyšel čitatel zlomku: 2x^2-x(a+1)+(a+3)
řešíme: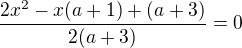
Zlomek je nulový, pokud je nulový čitatel: 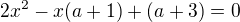 (a jmenovatel není nula, ale to jsme měli již v prvním kroku diskuse, že pro
(a jmenovatel není nula, ale to jsme měli již v prvním kroku diskuse, že pro 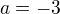 rovnice nemá smysl a úpravy provádíme pro
rovnice nemá smysl a úpravy provádíme pro 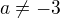 ].
].
M8me kvadratickou rovnici s parametrem 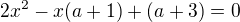 diskriminant D kvadratickou rovnice a provedeme diskusi počtu kořenů. Je to jasné, jak sestavit D? Děkuji.
diskriminant D kvadratickou rovnice a provedeme diskusi počtu kořenů. Je to jasné, jak sestavit D? Děkuji.
Offline
#11 25. 01. 2014 10:11
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: rovnice s paramtrem
↑ jelena: Jo Jo promin ten diskriminant mi vyšel  a potom stačí kdyz ten diskriminant rozdělil na součin a provedu diskusi ?
a potom stačí kdyz ten diskriminant rozdělil na součin a provedu diskusi ?
Offline
#12 25. 01. 2014 10:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice s paramtrem
↑ lukasstork:
ano, libovolnou metodou, kterou používáš pro vyšetření nulových bodů a znamének kvadratického trojčlenu (např. jak navrhuješ rozkladem na součin), provedeš diskusi počtu kořenů.
Pro interval, kde je jeden dvojnásobný a 2 kořeny, sestaviš i zápis pro kořeny  .
.
Offline
#13 25. 01. 2014 10:30
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: rovnice s paramtrem
↑ jelena: takže ty kořeny by mely byt  a
a  je to tak ?
je to tak ?
Offline
#14 25. 01. 2014 10:37 Příspěvek uživatele lukasstork byl skryt uživatelem lukasstork.
#15 25. 01. 2014 10:39
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: rovnice s paramtrem
↑ lukasstork: promin
ma to bejt 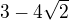 a
a 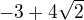
Offline
#16 25. 01. 2014 11:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice s paramtrem
lukasstork napsal(a):
↑ jelena: takže ty kořeny by mely byt
a
je to tak ?
ano, to jsou kořeny pro neznámou  v diskriminantu (nulové body pro
v diskriminantu (nulové body pro  ).
).
Teď můžeš rozklad na součin - máme, nebo tabulku, nebo číselnou osu. V příspěvku 15 to není dobře.
Offline
