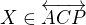Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2014 18:07
- janca361

- .
- Příspěvky: 3284
Konstrukční úloha
Ahoj,
na MA+ dnes byla tato úloha. Neznám nikoho, kdo by to vyřešil.
Úkolem je narýsovat trojúhelník ABC.
Strana AC je zadána. Dále vím, že  a
a  se protínají v bodě P (je zadán).
se protínají v bodě P (je zadán).
Náčrt (v testu to bylo přesně, tady je to "od oka", takže to nemusí vyjít, pokud by do toho někdo chtěl kreslit):
Mě napadla jen S(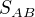 ): C->B. Jen střed ani žádnou jinou dvojici bodů, které by toto shodné zobrazené určily, nemám.
): C->B. Jen střed ani žádnou jinou dvojici bodů, které by toto shodné zobrazené určily, nemám.
(pro zajímavost: úloha za 3 body z celkových 50)
Offline
#2 02. 04. 2014 18:32 — Editoval gadgetka (02. 04. 2014 18:36) Příspěvek uživatele gadgetka byl skryt uživatelem janca361. Důvod: Taky mě to napadlo, jen ono P není těžiště.
#4 02. 04. 2014 18:45 — Editoval gadgetka (02. 04. 2014 18:48)
Re: Konstrukční úloha
Kdyby bylo zadání naopak, myslím tím  a
a  , bylo by to jednodušší. :)
, bylo by to jednodušší. :)
Ještě kdyby se sestrojil trojúhelník 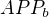 , kde
, kde 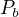 je pata výšky
je pata výšky  , tak pak trojúhelník
, tak pak trojúhelník 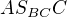 je mu podobný, ne? Nešlo by jít touto cestou?
je mu podobný, ne? Nešlo by jít touto cestou?
Strany by se změřily, našel by se koeficient podobnosti a pak by se lehce sestrojila celá strana BC a doplnil by se celý trojúhelník. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 02. 04. 2014 20:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukční úloha
↑ janca361:
Zdravím,
a) manual je třeba hledat s krátkým a,
b) Tebe osobně jsem z Manualu školila.
Skoro OT: zadání těžnice se obvykle spojuje s využitím středové souměrnosti. Zkusila bych sestrojit z bodu P kolmici na AC, což je "kousek"  , potom z bodu C rovnoběžku k
, potom z bodu C rovnoběžku k  , označím CC´. Prodloužit AP do průsečíku s CC´, což bude P´. Střed PP´ je střed AB. Může být? Děkuji.
, označím CC´. Prodloužit AP do průsečíku s CC´, což bude P´. Střed PP´ je střed AB. Může být? Děkuji.
Offline
#7 02. 04. 2014 23:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukční úloha
↑ janca361:
:-) tady školím. A záznam o školení máš přidán do Poznámky (plně souhlasím, že z cvičných důvodů ho upravíš).
K trojúhelníku - když trojúhelník doplníš na kosodélník a vyznačíš co se na co zobrazí ve středové souměrnosti se středem ve středu strany BC, tak to je vidět. Střed BC není bod P´, ale je ve středu úsečky PP´. No jistě na rozdíl ode mne vlastníš kružítko, tak to zrealizuješ.
Offline
#9 03. 04. 2014 09:48 — Editoval Honzc (03. 04. 2014 09:48)
Re: Konstrukční úloha
↑ janca361:
Taková logičtější konstrukce (i když v podstatě stejná jako od↑ jelena: - zdravím)
vzhledem k podobnosti trojúhelníků BP'C a SP''C takto:
Offline
#13 03. 04. 2014 23:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukční úloha
kolega Honzc napsal(a):
Taková logičtější konstrukce
Také pozdrav :-) Správná poznámka - mám naprostou absenci logiky - nebylo mi přiděleno, tedy nezbývá mi nic jiného, než standardizovat - např. zadání těžnice naznačuje užití středové souměrnosti, jak navrhuji. Tvůj návrh plyne z užití podobnosti a faktu, že těžnice půlí protější stranu - obdobně byl využit v této konstrukci.
↑ byk7:
přidej, prosím, který standard využíváš (nejlépe slovně), děkuji.
Offline
#14 04. 04. 2014 00:48
Re: Konstrukční úloha
Pozdravujem ↑ jelena:,
Co je to ten manual?
Kde sa da citat?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 04. 04. 2014 00:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukční úloha
↑ vanok:
Zdravím, to je manual pro mat. fórum, co jsme sepsali na MatWiki.
Offline
#16 04. 04. 2014 01:05
Re: Konstrukční úloha
↑ jelena:
Dakujem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 04. 04. 2014 16:03 — Editoval Eratosthenes (04. 04. 2014 21:06)
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: Konstrukční úloha
↑ janca361:
Tady přece stačí využít jednoduché vlastnosti rovnoběžníka:
Černé přímky jsou dané, body D, C se snadno sestrojí jako vrcholy rovnoběžníka. Bod C je hledaným vrcholem, protože leží na dané výšce a úhlopříčka BC je půlena druhou úhlopříčkou rovnoběžníka - těžnicí hledaného trojúhelníka.
PS: Dodatečně jsem si všiml, že na obrázku mám obráceně body B a C. Na řešení to naštěstí nemá vliv:-)
Budoucnost patří aluminiu.
Offline
#18 04. 04. 2014 23:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukční úloha
↑ Eratosthenes:
Zdravím a děkuji za další možnost - i když není to variace na téma "užití středové souměrnosti"? ↑ příspěvek 5:, ↑ příspěvek 7:.
Na úloze je spíš ze standardizačního hlediska zajímavé, že co do podstaty zadání je zcela shodna s úlohou, ale zadání průsečíků prvků místo samotných prvků zadání mírně zneprůhlednilo. ↑ janca361: lze označit za vyřešené?
Offline
#19 05. 04. 2014 13:22
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: Konstrukční úloha
↑ jelena:
>> není to variace na téma "užití středové souměrnosti"? ↑ příspěvek 5:, ↑ příspěvek 7:.
Variace to asi je, ale neřekl bych, že ↑ příspěvek 5:, ↑ příspěvek 7: využívají středové souměrnosti, spíš jde o střední příčku trojúhelníka.
>> co do podstaty zadání je zcela shodna s úlohou...
Nesouhlasím. Zde není zadána ani velikost výšky, ani velikost těžnice, ale směr těchto příček, což je zcela jiná úloha.
Budoucnost patří aluminiu.
Offline
#20 06. 04. 2014 14:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukční úloha
↑ Eratosthenes:
děkuji, ne, střední příčku nevyužívám, dokresluji obraz trojúhelníku ABC ve středové souměrnosti se středem strany BC (a této souměrnosti i ostatní prvky).
Shoda je v postupu kolegů použití podobnosti trojúhelníků. Samotné zadání délek těžnice a výšky nedává možnost sestrojení, ale "domyšlení" průsečíku těžnice a výšky již dává. Ale je možné, že to překombinovávám.
Kolega vanok byl tak laskav a upozornil mne na materiál, který systematizoval konstrukce trojúhelníku (je to starší časopis v ruštině, tak nevím, zda by byl zájem o náhled). Údajně autor sestavil veškeré kombinace prvků, podle kterých jde sestrojit. Našel celkem 350 různých zadání. Je něco podobného v jiných řečích (tento materiál znám)? Děkuji a zdravím.
Offline
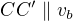 a zrovna
a zrovna  .
.

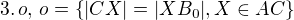
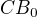 ,
,