Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Pravděpodobnost (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 05. 2014 12:25
Pravděpodobnost
Ahoj :) Mohla bych se zeptat, jak byste řešili tohle? X, Y jsou nezávislé náhodné veličiny. X má rovnoměrné rozdělení na intervalu 0,1 a Y rovnoměrné na intervalu -1,1. Spočtěte E [X+Y^2|X] a E[X+Y^2|X+Y] - podmíněné střední hodnoty...
Děkuju moc za jakýkoli nápad :)
Offline
- (téma jako vyřešené označil(a) byk7)
#2 27. 05. 2014 10:56
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Pravděpodobnost
K první střední hodnotě: E [X+Y^2|X] = E [X|X] + E [Y^2|X] = E [X] + E [Y^2].
Podmíněná střední hodnota E [X|X] = E[X] z definice, podmíněná střední hodnota E [Y^2|X] = E [Y^2], protože náhodné veličiny X a Y jsou nezávislé. Výsledné střední hodnoty se pak snadno spočítají integrací -).
Offline
#3 27. 05. 2014 18:06
#7 28. 05. 2014 10:51 — Editoval Brano (28. 05. 2014 13:07)
Re: Pravděpodobnost
Mr.Luc napsal(a):
↑ Stýv:
Ahoj,
samozřejmě platí:,
a s tymto mam zase ja problem - aj ked je to len vec volby domeny - teda ja som isiel podla definicie na wiki http://en.wikipedia.org/wiki/Conditiona … torization
(tej  z vety co tam je)
z vety co tam je)
keby sme zobrali ten vyraz so zamenenymi premennymi o par riadkov dalej t.j. 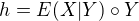 tak potom by sme pre
tak potom by sme pre  dostali
dostali  .
.
Tak pripadne napis aku pouzivas formalnu definiciu. Aj ked skor by to asi mala napisat OP, kedze sa to tyka jej prikladu.
EDIT: len by som rad zdoraznil, ze s podmienenou strednou hodnotou som nikdy nerobil, takze neviem ako sa to zvykne bezne prednasat "u nas" a ako sa s nou bezne pracuje, tak za to som isiel iba podla wiki a je aj sanca, ze som tam nieco zle pochopil. Ale myslim, ze je tam pomerne jasne napisane, ze definicny obor funkcie ![kopírovat do textarea $E[X|Y]$](/mathtex/e5/e545f66951cd184467c5ca6bd7d2e3d0.gif) je taky isty ako obor hodnot funkcie
je taky isty ako obor hodnot funkcie  , ktory teda nieje nutne taky isty ako definicny obor
, ktory teda nieje nutne taky isty ako definicny obor  .
.
Offline
#9 28. 05. 2014 18:04
Re: Pravděpodobnost
↑ Brano: definici podmíněný střední hodnoty máš o kus výš: http://en.wikipedia.org/wiki/Conditiona … definition
ta věc s kulatýma závorkama místo hranatých je něco jinýho. to se tuším používalo tak, že se podle nějakýho vzorečku spočítala ta fce g a pak se použilo E[X|Y]=g(Y). už je to taky nějakej pátek, co jsem se to učil, takže detaily ti nepovim
Offline
#11 28. 05. 2014 23:43 — Editoval Brano (29. 05. 2014 00:00)
Re: Pravděpodobnost
↑ Stýv:
hej uz som si to vsimol, ze oni tam tym malickym pismom potom definuju![kopírovat do textarea $E[X|Y]=E[X|Y^{-1}(\Sigma)]$](/mathtex/1b/1bc8cc11daffe6a7990d53041e8afe70.gif)
ale potom je tam vlastne dalej dokazane, ze to co som vlasne myslel ja t.j. 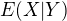 je v priamom vztahu s
je v priamom vztahu s ![kopírovat do textarea $E[X|Y]$](/mathtex/e5/e545f66951cd184467c5ca6bd7d2e3d0.gif) a to tak, ze
a to tak, ze ![kopírovat do textarea $E[X|Y]=E(X|Y)\circ Y$](/mathtex/79/799543045c1acd676a1dcbb65b9a1538.gif)
a to co som ja pisal, je teda toto (a teraz uz opravujem a davam gulate zatvorky aby som to rozlisil)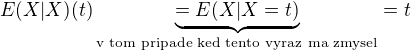 cize
cize cize
cize ![kopírovat do textarea $E[X|X]=id\circ X=X$](/mathtex/3e/3e6878c527867c3e98330b07f03e31f5.gif) a uz sa konecne zhodneme.
a uz sa konecne zhodneme.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Pravděpodobnost (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $E[X]$](/mathtex/6a/6a99d952029ee1846f251454ed19d6ac.gif) je cislo a
je cislo a ![kopírovat do textarea $E[X|X]$](/mathtex/52/52805dca351155bda362471383c41f9d.gif) je funkcia taka, ze
je funkcia taka, ze =E[X|X=t]=t$](/mathtex/d3/d308b7df474ae37a2952fba0ae35f62f.gif) .
.