Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Statistický operátor pro systém ve stavu termodynamické rovnováhy
#1 15. 10. 2014 23:09
- quagissimo

- Zelenáč
- Příspěvky: 3
- Škola: MFF UK
- Pozice: studentka
- Reputace: 0
Statistický operátor pro systém ve stavu termodynamické rovnováhy
Dobrý den, potřebovala bych poradit s jedním příkladem z kvantové mechaniky. Zadání zní:
Nalezněte statistický operátor  pro systém ve stavu termodynamické rovnováhy, tj. pravděpodobnost alezení libovolného stavu s vektorem |i> a energií E
pro systém ve stavu termodynamické rovnováhy, tj. pravděpodobnost alezení libovolného stavu s vektorem |i> a energií E je dáno pravděpodobností w
je dáno pravděpodobností w = \frac{1}{Z}e
= \frac{1}{Z}e \frac
\frac _{i}
_{i} , kde Z = \sum_{i} {e
, kde Z = \sum_{i} {e \frac
\frac _{i}
_{i} }.
}.
Předem Všem děkuji za jakoukoliv pomoc se řešením.
Offline
#2 15. 10. 2014 23:39
- misaH
- Příspěvky: 13459
Re: Statistický operátor pro systém ve stavu termodynamické rovnováhy
↑ quagissimo:
Ahoj.
To naozaj nevidíš, že text je nečitateľný?
Offline
#3 16. 10. 2014 10:46
Re: Statistický operátor pro systém ve stavu termodynamické rovnováhy
↑ misaH:
Dobrý den. Chtěla jste napsat toto?
quagissimo napsal(a):
Dobrý den, potřebovala bych poradit s jedním příkladem z kvantové mechaniky. Zadání zní:
Nalezněte statistický operátorpro systém ve stavu termodynamické rovnováhy, tj. pravděpodobnost nalezení libovolného stavu s vektorem |i> a energií
je dáno pravděpodobností
, kde
.
Předem Všem děkuji za jakoukoliv pomoc se řešením.
Pokud se tedy nemýlím.
Offline
#5 17. 10. 2014 20:44 — Editoval Brzls (18. 10. 2014 18:00)
Re: Statistický operátor pro systém ve stavu termodynamické rovnováhy
↑ quagissimo:
Čau
Nevím jestli je to nejlepší řešení, ale vcelku si myslím, že by mohlo fungovat. Netuším jak se takovéhle příklady řeší takže možná to lze nějak lépe.
Nechť H je hamiltonián a E_i jsou vlastní čísla této matice. Pak zvolme bázi tvořenou z jeho vlastních vektorů, v ní by mělo platit (pokud se nepletu) 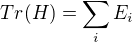 . kde Tr značí stopu matice
. kde Tr značí stopu matice
Dále víme, že z definice musí platit 
No a teď přijdou na řadu úpravy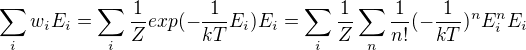
Podle anglické wikipedie platí dvě takové pěkné věci (první je jasná, té druhé prostě věřím, dokázat to fakt neumím)-edit: vlastně je to v našem případě triviální důsledek toho že máme matici v diagonálním tvaru a definice násobení matic)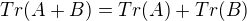

kde alfa_i jsou vlastní čísla dané matice (viz http://en.wikipedia.org/wiki/Trace_(linear_algebra)#Trace_of_a_linear_operator )
No a s tím můžeme pracovat dál když víme že ty energie jsou vlastní čísla hamiltoniánu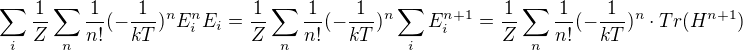
Teď si všimneme, že se všechno před Tr jsou konstanty a jediná operace sčítání, takže Tr můžeme napsat na začátek celého toho výrazu.
Poslední úprava zpět na exponenciálu dá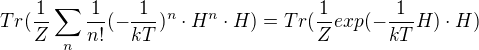
Tím jsme ale dostali vztah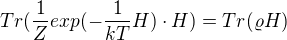
a proto bych usoudil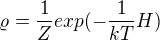
Jak říkám třeba to jde jednodušeji ale nikdo nic nepsal tak jsem si řekl že když jsem to nakonec nějak umlátil tak to sem hodím.
Téma přesunu do Zajímavých a náročnějších, třeba se ozve někdo zkušenější
Offline
#8 17. 10. 2014 23:52
Re: Statistický operátor pro systém ve stavu termodynamické rovnováhy
↑ pietro:
Děkuji
Tak jsem ještě zapátral v českých zdrojích a vypadá to že i česká wikipedie s výsledkem souhlasí (viz poslední odstavec)
http://cs.wikipedia.org/wiki/Oper%C3%A1tor_hustoty
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Statistický operátor pro systém ve stavu termodynamické rovnováhy
