Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Parna, neparna, licha, suda funkcia
#1 13. 11. 2015 13:35
Parna, neparna, licha, suda funkcia
Pozdravujem,
Toto cvicenie sa mi zda sokujuce
http://forum.matweb.cz/viewtopic.php?id=87473
Ako je mozne , ze dnes ked pojem funkcie je dobre znamy (a dobre vyucovany) miesat pojem funcie a jej hodnotu v bode x: f(x)
Nieto take toleruje ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 13. 11. 2015 18:39
Re: Parna, neparna, licha, suda funkcia
↑ vanok:
Já v tom nevidím problém, je to věc dohody značení. A Vojtěch Jarník v Diferenciálním počtu I, 6. vydání z roku 1974 na str. 148 v tom taky problém nevidí.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 13. 11. 2015 18:55
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Parna, neparna, licha, suda funkcia
ahoj ↑ vanok:,
Podle ustálených zvyklostí (není-li řečeno jinak), písmena z konce abecedy značí proměnné. Pro konstanty máme začátek abecedy, anebo indexy. Tedy
f(x) je funkce proměnné x,
f(a) f(x_1) jsou funkční hodnoty funkce f v bodech a resp. x_1
Budoucnost patří aluminiu.
Offline
#4 13. 11. 2015 19:46 — Editoval vanok (13. 11. 2015 19:48)
Re: Parna, neparna, licha, suda funkcia
↑ Pavel:, ↑ Eratosthenes:
Mozno pre 50 rokmi pojem funkcie nebol dostatocne jasno vypracovany, tak v tej dobe aj niektori matematici robili nepresne dohody (ako to poznamenal ↑ Pavel:)
No dnes, uz nikto nerobi taketo nepresnosti.
Dohody, ktore mozu znechutit aj mudrich ludi z matematiky nie su idealne.
Lokalna zvyklost, ked je nepresna, treba robit vsetko aby zmizla.
A nestaci, ze take zvyklosti pozostavali este v jednej ci dvoch zemiach, ze v nich treba pokracovat.
Ako sa k tomu vyjadruju k tomu vase osnovy?
Pisu sa u vas, ine veci ako skandalozne testy na niektorych skolach, z takymito zlozvykmi?
Vam sa skutocne toto pacî?
Necitate moderne knihy z inych zemi ?
Zda sa mi, ze si robite zo mna svandu !!!!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 13. 11. 2015 21:18 — Editoval Eratosthenes (13. 11. 2015 21:19)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Parna, neparna, licha, suda funkcia
↑ vanok:
nějak tě to rozhodilo - nad tvojí reakcí mi rozum zůstal stát a stojí ještě teď. Jestliže ti to jako moudrému člověku znechucuje matematiku, nikdo tě nenutí, abys to četl.
Jsem rád, že já takto "moudrý" nejsem. Mně naštěstí matematiku neznechutí nikdy nic. Ani tvoje zuřivé a neuvážené výkřiky.
Budoucnost patří aluminiu.
Offline
#6 13. 11. 2015 21:23 — Editoval Pavel (13. 11. 2015 21:24)
Re: Parna, neparna, licha, suda funkcia
↑ vanok:
Pojem funkce je ustálený už od 18. století. Asi nebudeme podezřívat Jarníka, žáka Landaua, že by v tom měl nejasno.
Nemá smysl zkoumat, zda je dohoda přesná nebo nepřesná. Dohoda musí být hlavně jasná, aby jejím ustanovením nedošlo k mylné interpretaci. Je zřejmé, že tím může utrpět preciznost matematického textu. Častým cílem takových dohod je zjednodušit text ve prospěch jeho srozumitelnosti.
Budu-li hovořit o funkci  , byť by správnější mělo být o funkci
, byť by správnější mělo být o funkci  , nemůže dojít k nedorozumění, protože je jasné, že právě předpisem
, nemůže dojít k nedorozumění, protože je jasné, že právě předpisem 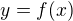 (a definičním oborem) je funkce
(a definičním oborem) je funkce  jednoznačně určena. Umožňuje mi to pak používat symbol
jednoznačně určena. Umožňuje mi to pak používat symbol  nejen jako hodnotu druhé mocniny v bodě
nejen jako hodnotu druhé mocniny v bodě  , ale i jako samotný objekt funkce druhá mocnina, viz též moderní kniha
, ale i jako samotný objekt funkce druhá mocnina, viz též moderní kniha
Anthony W. Knapp, Basic Real Analysis, 2005, Birkhäuser, ISBN 978-0-8176-3250-2, str. 11, Example předcházející Theorem 1.10.
Takových dohod je v matematice spousta a na první pohled se může zdát, že jsou nelogické.
Např. je-li  , pak
, pak 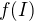 se interpretuje jako množina funkčních hodnot
se interpretuje jako množina funkčních hodnot  , kde
, kde 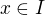 , i když samotný symbol
, i když samotný symbol 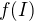 , bráno přísně formálně, nemá smysl.
, bráno přísně formálně, nemá smysl.
Operátor  označuje jednou součin, např.
označuje jednou součin, např. 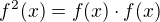 , podruhé skládání, např.
, podruhé skládání, např.  , kde
, kde  je čtvercová matice reprezentující jisté lineární zobrazení.
je čtvercová matice reprezentující jisté lineární zobrazení.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 13. 11. 2015 22:03
Re: Parna, neparna, licha, suda funkcia
Moj mily ↑ Eratosthenes:,
Ja ti kludne pisem.... Kde vidis zurivost ? Kde vidis ze kricim. Ja len konstatujem.
Ze sa snazis tvojou ironiou urazat inych to ti necham. No pisny by som na to nebol.
Pocul si niekedy o diskuziii ?
Pises o dohodach, a kde taka dohoda existuje? Za to, ze nieco sa pouzivalo v jednej knihe co viac ako 40 rokov, to neznamena, ze sa to musi byt tak aj dnes. (Vela veci sa od vtedy vyvinulo)
Kde som napisal, ze mi to znechucuje matematiku. Ja som napisal nieco ine!!!!!!
Vidim, ze nechces pochopit co pisem a ze nechces ist z dobou.Pozri na dnesne knihy z matematiky a uvidis ze nikto nepouziva tu skandaloznu dohodu
Skoda, ze si si to nevsimol.
Na co je to dobre, ze sa snazis deformovat co som napisal, skor sa mi zda, ze nechces ( ci nedokazes ?) rozumiet co pisem.
.
Miesat hodnotu funkcie z funkciou je chyba. Nich ine som nepovedal. ( No na to treba vediet ako je definovana funkcia)
Ked sa vidi nieco co nie je ako treba, tak to treba povedat.
Na dnes vecer to staci.
Tak dobru noc moj mily ↑ Eratosthenes:.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 13. 11. 2015 22:32 — Editoval vanok (14. 11. 2015 07:50)
Re: Parna, neparna, licha, suda funkcia
↑ Pavel:
Pozdravujem,
Ano su, situacie kde je to jasne.
Co sa tyka Jarnika, v tej dobe , ked pisal jeho knihy nebolo este bezne pouzivat funkciu v sipkovom oznaceni ( zda sa , ze to prvy uviedol
Ale co je skutocne pravda, v fr, enl, us. kde v rokoch 60, 70 presla vlna modernej matematiky vo vyucovany na vsetkych stupnoch skol, a to mozno aj u beznych ludi zanechalo stopy, ako aj co sa tyka funkcie. To sa asi u vas nerobilo v takej miere. ( tak ci tak taketo reformy sa ukazali priliz abstraktne a uz do 1980 skoro nic z nich neostalo) https://en.m.wikipedia.org/wiki/New_Math ( pridane Edit 14/12 )
Ale, co je iste, ze dohody, ktore mozu viest k nepresnostiam pomaly miznu
Ale hovorit v didaktike o nepresnich situaciach je iste uzitocne.
Mas pravdu pozname vela takych situacii, ale pokial ide o zjednodusnia, to je pozitivne na vyjadrenie... a vsetci ich pouzivame.
Iny zaujimavy fenomen je ze zmena oznaceni moze niekedy dat iny pohlad na niektore vlasnosti. Ale o tom iste podiskutujeme v inom vlakne.
Tak dobru noc.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 13. 11. 2015 22:55 — Editoval Pavel (13. 11. 2015 23:02)
Re: Parna, neparna, licha, suda funkcia
↑ vanok:
Neměl jsem na mysli nějaké obecně platné dohody. Spíše šlo o dohody, které sjednává autor publikace, knihy, přednášky, se čtenářem, posluchačem, studentem. Jsou často v učebních textech.
Např. místo přesnějšího zápisu "Nechť je dána funkce  určená předpisem
určená předpisem 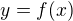 " budeme v dalším textu zkráceně psát "Nechť je dána funkce
" budeme v dalším textu zkráceně psát "Nechť je dána funkce  ".
".
Jinak argument, že je třeba jít s dobou, neberu. Doba nemá s diskutovaným problémem nic společného. Je to spíš otázka konvence.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#10 13. 11. 2015 23:24 — Editoval vanok (13. 11. 2015 23:28)
Re: Parna, neparna, licha, suda funkcia
↑ Pavel:
To je tazko sudit.
Ked citam knihy z 1850 tak to je gymnastika na ich dohody
Ucebne texty to asi nie je problem....
Ozaj ako popisoval, napr Jarnik pojem funkcie
Pozeral som Hardy, ten ma celkom moderny popis.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 14. 11. 2015 10:48 — Editoval Eratosthenes (14. 11. 2015 11:53)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Parna, neparna, licha, suda funkcia
↑ vanok:
>> Ja ti kludne pisem...
a při tom "klidném psaní" používáš výrazy jako "znechucení", "skandal" a čtyři vykřičníky za poslední větou...
>> Miesat hodnotu funkcie z funkciou je chyba. Nic ine som nepovedal.
To se pleteš. Ty jsi řekl, že dohoda "f(x)=funkce, f(a)=funkční hodnota" je skandál, který znechucuje od matematiky a že si z tebe děláme srandu.
>> Necitate moderne knihy z inych zemi?
Nevím, co má tato otázka společného s tématem. Tobě stačí "prečítat Hardy" a hned víš, co a jak dělá celý moderní svět a taky víš, že jedině to je ono, že tak je to spravne a tak to ma byt, protože všechno ostatní je lokální a špatné. Takové názory dělají jenom paseku. A nejenom v matematice.
>> Vidim, ze nechces pochopit, co pisem.
Já mám spíš pocit, že to chápu až moc dobře.
>> Nikto nepouziva tu skandaloznu dohodu...
Na matematika si až příliš často pleteš existenční a obecný kvantifikátor. Jako matematik bys měl vědět, že k vyvrácení takto kategorických tvrzení, stačí jeden jediný protipříklad. Tím můžu být třeba já. Ale abys neřekl, že to beru příliš doslova, tak ještě "moderní zahraniční texty", které tak často bereš jako důkaz svých tvrzení. Tak tedy první, na který jsem narazil:
Z toho plyne, že tvoje tvrzení "Nikto nepoužívá..." je zcela jistě nepravdivé.
Budoucnost patří aluminiu.
Offline
#12 14. 11. 2015 11:49
Re: Parna, neparna, licha, suda funkcia
↑ Eratosthenes:
Skutocne nerozumies co som pisal... Viem jedine, ze chces mat za kazdu cenu pravdu.
Tak ti tu tvoju pravdu necham, ked je pre teba take dolezite mat vzdy pravdu, aj ked realita moze byt ina.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 14. 11. 2015 18:35
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Parna, neparna, licha, suda funkcia
↑ vanok:
matematika mě naučila, že pravda se nedá nechávat. Tu lze jen dokázat, anebo vyvrátit. A vždycky ji nemám. Nemám ji tehdy, když mi to někdo dokáže. Několikrát se to stalo i na tomto fóru...
Budoucnost patří aluminiu.
Offline
#14 14. 11. 2015 18:47
Re: Parna, neparna, licha, suda funkcia
↑ Eratosthenes:
Gratulujem, ze aspon v jednej oblasti si schopny napredovat. Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 30. 11. 2015 19:36
Re: Parna, neparna, licha, suda funkcia
Zdravím v zajímavém tématu.
Ačkoliv mi občas také vadí psaní  místo
místo  , v principu se přikláním k názorům Pavla a Eratosthena. Podle mého názoru totiž korektnost matematického formalismu nemá být pánem, ale sluhou. Ať je zápis klidně trochu nekorektní, pokud to zpřehlední situaci a nevznikne riziko, že by mohlo dojít k mylné interpretaci. Ať si každý píše a říká co chce, pokud si je jistý, že to posluchači a čtenáři budou interpretovat správně a budou vědět, jak to v případě potřeby korektně matematicky zapsat.
, v principu se přikláním k názorům Pavla a Eratosthena. Podle mého názoru totiž korektnost matematického formalismu nemá být pánem, ale sluhou. Ať je zápis klidně trochu nekorektní, pokud to zpřehlední situaci a nevznikne riziko, že by mohlo dojít k mylné interpretaci. Ať si každý píše a říká co chce, pokud si je jistý, že to posluchači a čtenáři budou interpretovat správně a budou vědět, jak to v případě potřeby korektně matematicky zapsat.
To je však jen jedna stránka mince. Problém totiž je, že mnoho lidí používá nekorektních zápisů i v případech, kde to nemá žádný smysl a nevede to k zpřehlednění.
Třeba v případě úlohy, na kterou odkazuje vanok, si myslím, že používání chybného zápisu nepřináší žádný užitek, takže bych tam rozhodně radši viděl zápis korektní.
Další problém je, že (podle mé zkušenosti) si hodně lidí ani neuvědomuje, že se psaním  místo
místo  fakticky dopouští chyby. Z velké části je to asi způsobeno tím, že na středních školách se samotné
fakticky dopouští chyby. Z velké části je to asi způsobeno tím, že na středních školách se samotné  nebo
nebo  vyskytne velice zřídka. Studentům jsou vtloukány do hlavy i nesmysly takového typu, že symbol
vyskytne velice zřídka. Studentům jsou vtloukány do hlavy i nesmysly takového typu, že symbol  nemá sám o sobě žádný smysl a je nutné vždy psát
nemá sám o sobě žádný smysl a je nutné vždy psát  .
.
Offline
#16 30. 11. 2015 19:54
Re: Parna, neparna, licha, suda funkcia
↑ Jenda358:
Takže když bych chtěl ten tvůj případ se sinem napsat korektně, tak musím psát ![kopírovat do textarea $\sin:\mathbb{R}\to[0,1]$](/mathtex/07/0794109bc48c8c5308310bbbdad68ad8.gif) a
a 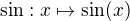 ?
?
Ne, že bych v tom viděl chybu, ale takový styl zápisu jsem nikdy neviděl a přijde mi poněkud zvláštní (ale jak říkám, pouze můj názor).
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#17 30. 11. 2015 21:43
Re: Parna, neparna, licha, suda funkcia
Ahoj ↑ byk7:,
Dobry zapis je napr.![kopírovat do textarea $\sin:\mathbb{R}\to[0,1]$](/mathtex/07/0794109bc48c8c5308310bbbdad68ad8.gif)

Uvaz vyhody a nevyhody....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 01. 12. 2015 21:21
Re: Parna, neparna, licha, suda funkcia
↑ byk7:
Ano, i když ještě víc se mi líbí to, co napsal vanok.
Důvod, proč ti takovýto zápis připadá zvláštní, je, že není (bohužel) obvyklý. Je však zcela logický a je v souladu s pravidlem, že symbol  označuje hodnotu funkce
označuje hodnotu funkce  v bodě
v bodě  .
.
Pamatuju si, že když jsem před dvěma lety na matfyzu začínal, tak jsem byl přinejmenším překvapen, když jsem spatřil zápisy typu 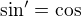 . Ale rychle jsem si zvyknul.
. Ale rychle jsem si zvyknul.
Offline
#19 01. 12. 2015 22:08
Re: Parna, neparna, licha, suda funkcia
↑ Jenda358:
Nabízí se pak otázka, zda stejné označení používat pro funkci druhé odmocniny, resp. mocniny. Budeme tedy hovořit o funkci , resp.  ? Jak potom zapisovat exponenciální funkci o základu 5? Jako
? Jak potom zapisovat exponenciální funkci o základu 5? Jako  ? A jak vůbec zapisovat polynomickou funkci? To už vůbec nezmiňuji funkce dvou a více proměnných.
? A jak vůbec zapisovat polynomickou funkci? To už vůbec nezmiňuji funkce dvou a více proměnných.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#20 01. 12. 2015 23:04
Re: Parna, neparna, licha, suda funkcia
Ahoj ↑ Pavel:,
Mas uplne pravdu, "skratene " oznacenia pre funkciu mozu az nezrozumitelne.
Zapis ako![kopírovat do textarea $f:\mathbb{R}\to[0,1]$](/mathtex/c1/c10a44545eba4663c8cbe7bc0162ce59.gif)

cely oznaci funkciu o ktory ide. Napisat len f, alebo iny symbol ma podobne nepresnosti ako tie o ktorych sme hovorili vyssie.
Tiez, co sa tyka miesania pojmov funkcia polynom, a algebricky polynom, casto je dostatocne zrozumitelne (podla struktur na ktorych su definovane) no vsak niekedy nie je mozne ztotoznit tieto dva pojmy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 02. 12. 2015 00:38
Re: Parna, neparna, licha, suda funkcia
Zdravím všechny v tématu.
Pokud bych měl psát do nějakého článku, určitě bych důsledně dodržoval rozlišení mezi  a
a  - už jen z formálního hlediska je to prostě chyba. Překladač každého staticky typovaného programovacího jazyka to taky nezkousne, což je ve skutečnosti výhodné, protože to umožňuje rychle najít chybu. To samý podle mě platí ve složitějších matematických situacích - autorovi to poskytuje větší kontrolu nad tím, co dělá. Např. ve funkcionální analýze je podle mě tohle rozlišování naprosto nezbytné. Když chci třeba pracovat s kanonickým zobrazením do druhýho duálu, tak potřebuju psát věci jako
- už jen z formálního hlediska je to prostě chyba. Překladač každého staticky typovaného programovacího jazyka to taky nezkousne, což je ve skutečnosti výhodné, protože to umožňuje rychle najít chybu. To samý podle mě platí ve složitějších matematických situacích - autorovi to poskytuje větší kontrolu nad tím, co dělá. Např. ve funkcionální analýze je podle mě tohle rozlišování naprosto nezbytné. Když chci třeba pracovat s kanonickým zobrazením do druhýho duálu, tak potřebuju psát věci jako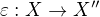 ,
, 
a už tady bych byl v koncích, kdybych důsledně nerozlišoval  a
a  .
.
Jediná neýhoda tohoto přístupu je to, co už tu někdo zmínil, že některé jednoduché funkce jako  musí člověk opisovat jako
musí člověk opisovat jako  nebo podobně. Někdy se ještě dá použít
nebo podobně. Někdy se ještě dá použít  , např.
, např. 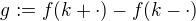 , někdy ne. Vesměs ale tyhle komplikace jsou naprostý drobnosti.
, někdy ne. Vesměs ale tyhle komplikace jsou naprostý drobnosti.
Na střední škole mi to zaměňování funkce s její funkční hodnotou přijde pochopitelné, protože se se vším začíná na příkladech a zrovna ty "problematické" funkce jako  ,
,  ,
, 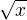 jsou ty nejjednodušší příklady a člověk si tak nějak prostě zvykne tam psát to x. Když pak někde vidí
jsou ty nejjednodušší příklady a člověk si tak nějak prostě zvykne tam psát to x. Když pak někde vidí 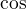 , tak mu to připadá hrozně divný. Tím to ale nechci nijak obhajovat, jen nabízím svůj názor na to, jak tahle chyba vzniká.
, tak mu to připadá hrozně divný. Tím to ale nechci nijak obhajovat, jen nabízím svůj názor na to, jak tahle chyba vzniká.
Offline
#22 02. 12. 2015 15:43 — Editoval Jenda358 (02. 12. 2015 15:44)
Re: Parna, neparna, licha, suda funkcia
Pavel napsal(a):
↑ Jenda358:
Nabízí se pak otázka, zda stejné označení používat pro funkci druhé odmocniny, resp. mocniny. Budeme tedy hovořit o funkci , resp.? Jak potom zapisovat exponenciální funkci o základu 5? Jako
? A jak vůbec zapisovat polynomickou funkci? To už vůbec nezmiňuji funkce dvou a více proměnných.
V případech mocninných nebo polynomiálních funkcí asi neexistuje rozumný způsob, jak vytvořit rozumný zápis analogický 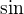 nebo
nebo 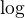 atd. Samozřejmě by šlo prostě vymyslet nové symboly nebo v případě odmocniny používat např.
atd. Samozřejmě by šlo prostě vymyslet nové symboly nebo v případě odmocniny používat např.  , nicméně je jasné, že vymýšlet stále další a další symboly by ničemu nepomohlo.
, nicméně je jasné, že vymýšlet stále další a další symboly by ničemu nepomohlo.
Proto bych se klonil k zápisům typu  apod.
apod.
Ale jak už jsem psal výše – myslím, že na prvním místě není korektnost zápisu, ale to, jestli ho čtenář či posluchač správně interpretuje a je si vědom, zda je ten zápis korektní či nikoliv. Mluvit o "funkci  " je velice pohodlné a každému je snad jasné, jak je to myšleno, takže bych to toleroval.
" je velice pohodlné a každému je snad jasné, jak je to myšleno, takže bych to toleroval.
V případě "funkce  " je to ale něco jiného, protože tam přece není žádný důvod vyhýbat se korektnímu značení. Psaní
" je to ale něco jiného, protože tam přece není žádný důvod vyhýbat se korektnímu značení. Psaní 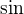 je korektní a zároveň přehledné a pohodlné.
je korektní a zároveň přehledné a pohodlné.
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Parna, neparna, licha, suda funkcia
