Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » vie tu niekto vysvetlit faktorialy ???? (TOTO TÉMA JE VYŘEŠENÉ)
#27 04. 06. 2009 08:49
Re: vie tu niekto vysvetlit faktorialy ????
↑↑ 7867088:↑↑ 7867088: Kdyz nekdo radi gamma funkci, vi o ni neco? A kdyz se nekdo bavi o tridach P a NP, vi o nich neco?
Offline
#28 04. 06. 2009 08:52
Re: vie tu niekto vysvetlit faktorialy ????
7867088 napsal(a):
7867088 napsal(a):
jinak já bych taky měl otázku: je faktoriál algoritmus P nebo NP, jen tak pro zajímavost ;-)
prosím, věděl by někdo?
Vzpomínám si, že už jsme spolu nějaké diskuze vedli a skončili jsme u toho, že na své správné používání termínů z VŠ matematiky si ještě chvilku budeš muset počkat. A tipl bych si, že podobně to bude pro termíny z teoretické informatiky.
Offline
#29 05. 06. 2009 12:40
Re: vie tu niekto vysvetlit faktorialy ????
Marian napsal(a):
Začátečník může ocenit jistě i tento materiál (pdf).
Kjuba
Měl jsem poznámku o symbolu * připravenu, ale nestihl jsem to. Opět to vypadá, že se blíží ***Vánoce***. Prosím, funguje příkaz \cdot - udělej si radost pro dnešek.
Hezke pdf, jen by me zajimalo jak se da spocitat bez kalkulacky toto:
69! = 1,71 . 10^98
Offline
#30 05. 06. 2009 17:28
Re: vie tu niekto vysvetlit faktorialy ????
Marian napsal(a):
Začátečník může ocenit jistě i tento materiál (pdf).
Kjuba
Měl jsem poznámku o symbolu * připravenu, ale nestihl jsem to. Opět to vypadá, že se blíží ***Vánoce***. Prosím, funguje příkaz \cdot - udělej si radost pro dnešek.
Zdravím,sem si to pročetl a nerozumím tomu,jak spočítat: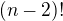
Poradte prosím
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#31 05. 06. 2009 17:35
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: vie tu niekto vysvetlit faktorialy ????
↑ Alivendes:
Tam není co počítat, to je prostě matematický výraz. Asi jako bys chtěla spočítat  . Zkus se podívat třeba sem: www.matweb.cz/faktorial
. Zkus se podívat třeba sem: www.matweb.cz/faktorial
2+2=4
Offline
#33 05. 06. 2009 17:39
#35 06. 06. 2009 21:42 — Editoval jelena (06. 06. 2009 21:47)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vie tu niekto vysvetlit faktorialy ????
↑ schriz:
Zdravím, rozepisuješ "vetší" faktoriály směrem k "menším" přesně podle doporučení kolegů v tématu ...
...
Nerovnici upravuješ na anulovaný tvar a také rozpis "větších" faktoriálů na "menší":

společný jmenovatel opět přepišu ve "zkráceném zápisu pro faktoriály
Výraz v jmenovateli je kladné pro každé x z definičního oboru. , kladný tedy musí být i čitatel, aby byla nerovnost splněna.
Definiční obor stanovíme tak, že každý výraz se znakém faktoriálu musí být nezáporný (faktoriál nuly a definitoricky :-)
Offline
#38 07. 06. 2009 11:21
Re: vie tu niekto vysvetlit faktorialy ????
↑ jelena:
Pokud jsou ve jmenovateli faktoriály, pak lze v nerovnici bez problémů eliminovat zlomky. Faktoriál z přirozeného čísla je vždy kladný.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#39 07. 06. 2009 11:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vie tu niekto vysvetlit faktorialy ????
↑ Pavel:
Zdravím,
Ty to víš, já to vím ↑ jelena: - napsala jsem to na závěr svého příspěvku (a definitoricky).
Ale nevím, zda takovou diskusi provede i nase kolegyně. Jednou dovolím jen tak násobít a pak to budu těžce vytloukávat. Ne. Proto byla moje kontrolní otázka. Jinak v otázce povolení násobení vždy se obrácim na Pavlův příspěvek č. 5 a pak jsem já pokračovala v příspěvku 6.
Děkuji za doplnění :-)
Offline
#41 08. 06. 2009 22:31 — Editoval jelena (24. 08. 2010 17:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vie tu niekto vysvetlit faktorialy ????
↑ schriz:
Zdravím,
když už jsem to rozpracovala, tak dokončím. Z úvodu tohoto tématu jsem pochopila, že s faktoriály teprve začínaš a nejsem si jistá, zda jsi dostatečně nastudovala pravě takové podrobnosti, na které upozorňuje a samozřejmě zcela správně ↑ Pavel:.
Bohužel, moje zkušenost je taková, že při řešení rovnic a nerovnic s neznámou v jmenovateli je lepší si zvyknout vždy převádět na anulovaný tvar (vše nalevo, 0 napravo, společný jmenovatel) a řešit celý zlomek.
U rovnice je dostačujici se zaměřit na podmínku, že jmenovatel nesmí být nulový, po tomto omezení již řešit 0 v čitateli.
U nerovnic je situace složitejší - rozebírá to dost podrobně pravě Pavel ve svém příspěvku č. 5. Zde jsme to rozebrali s kolegou halogan(em) a tady zas s kolegou liquid(em) - to byla doba, ovšem :-)
Už bych to všechno jen opakovala.
V tomto konkrétním případě doporučuji to, co jsem již řekla: 

 (to je jasné),
(to je jasné),
jmenovatel je kladný:  pro každé x, které splňuje podmínky:
pro každé x, které splňuje podmínky: 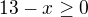 a
a 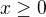 a
a  a
a 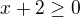 , to jest:
, to jest:
Musí být kladný čitatel, aby nerovnice byla splněna:


Pokud jsem neudělala nějakou chybu, tak x by mělo být přirozené číslo z intervalu: (5.5 , 11>
jinak receno {6, 7, 8, 9, 10, 11}
--------------------
Ale nejsem žádný profesionál v oboru matematiky, ani v oboru příbuzném, proto uvítám spravedlivou kritiku od profesionálů, děkuji.
пропадет, он говорил, моя буйна голова
původ textu
EDIT: opravila jsem odkaz na "So ends another day".
Offline
#42 09. 06. 2009 01:21
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: vie tu niekto vysvetlit faktorialy ????
↑ 7867088:Nejde o to, že by to byl nějak těžký dotaz, spíš se nehodí do sekce střední škola a už vůbec ne do tématu, kde je v plném proudu diskuse o úpravě výrazů, nikoliv o výpočetních složitostech. Něco jsem k tomu sepsal tady: http://forum.matweb.cz/viewtopic.php?pid=60923#p60923
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » vie tu niekto vysvetlit faktorialy ???? (TOTO TÉMA JE VYŘEŠENÉ)

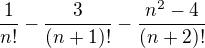

 ??
??