Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 13. 06. 2009 21:19 — Editoval gladiator01 (13. 06. 2009 21:59)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Nerovnice
edit: já jsem z toho zkouškového nějak mimo
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#5 13. 06. 2009 21:21
Re: Nerovnice
↑ gladiator01: no ja som v živote takto nerovnicu nepočítal...
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#6 13. 06. 2009 21:27
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Nerovnice
↑ Redvo:
Tvým způsobem ji ani nikdy nepočítej... není to správně :)
↑ gladiator01:
A co když x bude -10? Zkus se zamyslet nad tím, co jsi zapomněl.
Offline
#7 13. 06. 2009 21:31
Re: Nerovnice
↑ halogan: ok zapamätám si, cez nulové body :)
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#8 13. 06. 2009 21:32
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Nerovnice
↑ Redvo:
Ještě abys věděl proč - ty totiž nevíš, čím tu rovnici násobíš. Musel bys to rozdělit na dva intervaly a otáčet znamínka, ale to už je rychlejší řešení výše (byť nyní je ještě stále špatně).
Offline
#9 13. 06. 2009 21:35
Re: Nerovnice
↑ halogan: ale inak čo je na tej mojej nerovnici zle? veď vychádza či nie?
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#12 13. 06. 2009 21:45 — Editoval Redvo (13. 06. 2009 21:50)
Re: Nerovnice
↑ halogan: no a? ke%d doplním -10 a vydelím vide  a to je stále viac ako 2 pokiaľ sa nemýlim
a to je stále viac ako 2 pokiaľ sa nemýlim
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#15 13. 06. 2009 21:55
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Nerovnice
↑ Redvo:
Viz můj ↑ halogan: příspěvek.
Offline
#16 13. 06. 2009 21:56
Re: Nerovnice
ešte 1 otázka..sú všetky tieto opletačky okolo toho spôsobené tým že je to nerovnica s neznámou v menovateli? keby to bolo len napr  tak sa to musí riešiť cez nulové body? lebo sa mi zdá že takúto nerovnicu som vždy riešil ako aj rovnicu..len dal neznám,e na 1 a čísla na 2. stranu..
tak sa to musí riešiť cez nulové body? lebo sa mi zdá že takúto nerovnicu som vždy riešil ako aj rovnicu..len dal neznám,e na 1 a čísla na 2. stranu..
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#17 13. 06. 2009 22:02
#18 13. 06. 2009 22:03
Re: Nerovnice
↑ halogan: takže ďakujem za vysvetlenie, ešte som sa v živote nestretol s nerovnicou s neznámou v menovateli a tak som ju riešil ako rovnicu..aspoň budem do budúcna múdrejší, ešte raz ďakujem :)
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#19 13. 06. 2009 22:13
Re: Nerovnice
K tomu pocitani pres nulove body, je celkem kuriozni, ze poprve jsem se s tim setkal az na vysce. Nas ucitel, jinak docela kvalitni, se nam o tomto zpusobu reseni asi zapomnel zminit a my jsme vsechny takove rovnice pocitali podobne jako o kus vyse Redvo s tim, ze jsme si hlidali podminky. U slozitejsich prikladu to uz obcas vedlo docela ke zmatku, ale protoze jsme na to byli zvykli a nic jineho jsme neznali (protoze jsme ani nemeli potrebu vymyslet neco jineho), tak nam to stacilo.
Offline
#20 13. 06. 2009 23:14
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Nerovnice
A to jsou pak lepsi nerovnice s neznamou pod odmocninou ty se pak resi ruzne... A sloziteji...
viz. http://forum.matweb.cz/viewtopic.php?id=9665
Offline
#22 14. 06. 2009 10:10 — Editoval Redvo (14. 06. 2009 10:13)
Re: Nerovnice
↑ Kessi: spoločný menovateľ...
spoločný menovateľ  a musíš ním vynásobiť tú 2 ktorá mala ako menovateľa 1..zapíšem to takto:
a musíš ním vynásobiť tú 2 ktorá mala ako menovateľa 1..zapíšem to takto:  (-2).x= (-2x) a (-2).(-3)=+6 :)
(-2).x= (-2x) a (-2).(-3)=+6 :)
už tomu chápeš?ide len o spoločného menovateľa pri sčítaní zlomkov.. :)
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline



 skúška..dosadíš za x akékoľvek číslo podľa intervalu (od -4 do nekonečna)
skúška..dosadíš za x akékoľvek číslo podľa intervalu (od -4 do nekonečna)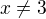




 :)
:)
 napíšeme ako
napíšeme ako 