Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pomalu alternující řada (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 03. 2010 22:02 — Editoval Olin (27. 03. 2010 17:24)
Pomalu alternující řada
Zdravím kolegy,
vyšetřoval jsem konvergenci řady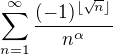
v závislosti na parametru  . Zajímavá je situace zejména pro
. Zajímavá je situace zejména pro 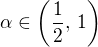 , kde by řada měla konvergovat. Můj postup byl následující:
, kde by řada měla konvergovat. Můj postup byl následující:
Je patrné, že členy řady změní znaménko právě tehdy, když je  čtvercem. Řadu tedy můžeme rozdělit na "souvislé úseky", které mají stejné znaménko:
čtvercem. Řadu tedy můžeme rozdělit na "souvislé úseky", které mají stejné znaménko: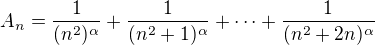 .
.
Není obtížné si rozmyslet, že z konvergence řady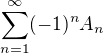
již plyne konvergence původní řady a naopak. Formát řady vybízí k použití Leibnizova kritéria - je tedy potřeba ověřit 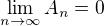 a
a  .
.
Konvergenci k nule ukážeme snadno, totiž odhadem  . Protože
. Protože  , je
, je 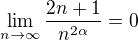 .
.
S monotónností to bude poněkud horší. První zjednodušení dostaneme odhadem integrály:![kopírovat do textarea $A_n \, > \int_{n^2}^{(n+1)^2} x^{-\alpha} \mathrm{d}x = \frac{1}{1-\alpha} \[ \((n+1)^2\)^{1-\alpha} - (n^2)^{1-\alpha} \] \nl A_{n+1} \, < \int_{(n+1)^2-1}^{(n+2)^2-1} x^{-\alpha} \mathrm{d}x = \frac{1}{1-\alpha} \[ \((n+2)^2-1\)^{1-\alpha} - \((n+1)^2-1\)^{1-\alpha} \]$](/mathtex/d9/d9401306f0061369d19eb80809d4eeed.gif) .
.
Označme 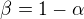 . Nyní bychom vlastně rádi dokázali
. Nyní bychom vlastně rádi dokázali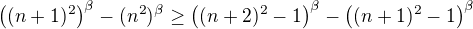 .
.
Upravujme:
Označíme-li 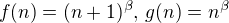 , pak podle Cauchyho věty o střední hodnotě existuje takové
, pak podle Cauchyho věty o střední hodnotě existuje takové 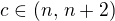 , že platí
, že platí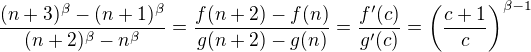 .
.
Díky faktu 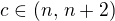 můžeme odhadnout
můžeme odhadnout 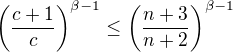 . Stačí tedy dokázat
. Stačí tedy dokázat
Zaveďme 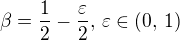 . Dostáváme
. Dostáváme
Ještě upravíme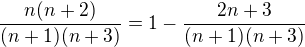
a použijeme Bernoulliho nerovnost: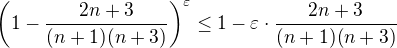 .
.
Zbývá tedy už jen nerovnost
která je již zřejmě od nějakého  dál splněna.
dál splněna.
Chybu jsem si v tom zatím nenašel. Ale ten postup je fakt škaredý na to, že po těch odhadech integrály už máme takovou docela snadno vypadající nerovnost. Tak kdybyste se někdo opravdu hodně nudili, můžete zkusit vymyslet nějaký hezčí postup, já v těch odhadech a nerovnostech příliš zběhlý nejsem.
EDIT: Opravena chyba. Kdo ví, kolik jich tam ještě je…
Offline
- (téma jako vyřešené označil(a) Olin)
#2 27. 03. 2010 15:48
Re: Pomalu alternující řada
↑ Olin:
[1] Souhlasím, že postup je dosti komplikovaný, ale dle mého názoru se příliš zjednodušovat nedá.
=============================
[2] Předně tuším formální chybu u obou integrálů - zřejmě integrujeme podle proměnné x a nikoliv  , což je fixní parametr.
, což je fixní parametr.
=============================
[3] Budu-li akceptovat definici čísla  , dokazoval bych místo nerovnosti
, dokazoval bych místo nerovnosti
raději nerovnost
která (jak se ukáže) platí pro všechna uvažovaná  od jistého
od jistého  , kde
, kde 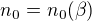 .
.
=============================
[4] K tomu stačí vyšetření funkce 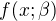 proměnné
proměnné  s parametrem
s parametrem  definované předpisem
definované předpisem
Odtud je
Odtud a z definice funkce f plyne
=============================
[5] Rádi bychom ukázali, že funkce 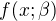 je od jistého
je od jistého 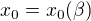 klesající, tj. ekvivalentně
klesající, tj. ekvivalentně
Pokud definujeme novou proměnnou  jako
jako 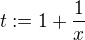 , lze poslední nerovnost zapsat jako
, lze poslední nerovnost zapsat jako![kopírovat do textarea $ t<(t+1)^\alpha,\qquad\qquad t\in (1,2],\qquad t\le t_0. $](/mathtex/d7/d72a999bd78bf737d024171fe5a5b27e.gif)
Odtud je vidět existence hledaného  .
.
=============================
[6] v důkazu nerovnosti 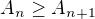 platící od jistého
platící od jistého  asi nelze postupovat jinak nebo zásadně jednodušeji. Spíše by se musela zvolit jiná metoda při vyšetřování samotné konvergence řady. Ovšem zde není příliš na výběr.
asi nelze postupovat jinak nebo zásadně jednodušeji. Spíše by se musela zvolit jiná metoda při vyšetřování samotné konvergence řady. Ovšem zde není příliš na výběr.
Offline
#3 27. 03. 2010 17:37
Re: Pomalu alternující řada
↑ Marian:
Děkuji za připomínky. Bod [2] jsem opravil. Postup pro dokázání nerovnosti, který předkládáš, mi přijde jako mnohem efektivnější.
Offline
#5 27. 03. 2010 21:20
Re: Pomalu alternující řada
To, že hraničním hodnotou alfy pro konvergenci je v tomto případě 1/2, dává podnět k vyšetření konvergence obecnější řady: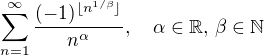 .
.
Až se mi někdy bude chtít, tak se do toho pustím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pomalu alternující řada (TOTO TÉMA JE VYŘEŠENÉ)

