Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » derivace výrazu s arccos (TOTO TÉMA JE VYŘEŠENÉ)
#3 09. 04. 2010 16:55 — Editoval Mara321 (09. 04. 2010 16:56)
Re: derivace výrazu s arccos
↑ Rumburak:
Nějak to nechápu, co znamena to u,v,w ?. Jsem zapomněl uvést, že y je funkce x, tedy výraz má být  , nebo chcete-li
, nebo chcete-li 
Offline
#4 09. 04. 2010 17:10
#5 09. 04. 2010 17:22 — Editoval Tomas.P (09. 04. 2010 17:59)
Re: derivace výrazu s arccos
Než abych ti poradil matematicky, tak ti poradím laicky.
Představ si nějakou starou kalkulačku (ne logaritmické pravítko),ve které nemůžeš závorkovat a ptám se :
Jakou operaci provedeš jako poslední, aby jsi došel ke správnému výsledku?
Poslední operaci, kterou by jsi provedl, aby jsi došel k výsledku, by byl v tvém případě součin.
Proto pokud chceš derivovat tebou zadaný výraz, musíš začít derivací součinu, potom můžeš přejít k derivaci složené fce.
Operace, která je u kalkulačky jako poslední, tak se jí u derivace začne
Pro větší přehlednost můžeš derivaci složené fce :  provést někde bokem podle návodu Rumburaka
provést někde bokem podle návodu Rumburaka
Offline
#9 09. 04. 2010 19:45
Re: derivace výrazu s arccos
↑ Mara321:když si v sekci vysokých škol klikneš na první zvýrazněné téma, tak dostaneš strojů víc..
Vesmír má čas.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » derivace výrazu s arccos (TOTO TÉMA JE VYŘEŠENÉ)

 , kde
, kde 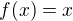 ,
,  .
. 
 ,
,  ,
,  .
.


