Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2010 10:46 — Editoval pizet (11. 04. 2010 10:53)
Geometrická postupnosť
Potreboval by som pomôcť s takýmto príkladom:
Pr] V geometrickej postupnosti poznáme prvý člen 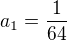 a kvocient
a kvocient 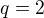 . Určte
. Určte  tak, aby platilo
tak, aby platilo 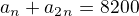 .
.
Zatiaľ som spravil toľko, že som si vyjadril 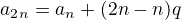 čo mi sedí ale neviem čo s tým ďalej...
čo mi sedí ale neviem čo s tým ďalej...
EDIT // no dosadil som to 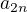 do prvej rovnice a použil som vzorec
do prvej rovnice a použil som vzorec 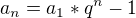 ale potom mi to divne vychádza...
ale potom mi to divne vychádza...
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
- (téma jako vyřešené označil(a) Dana1)
#2 11. 04. 2010 10:50 — Editoval Doxxik (11. 04. 2010 10:53)
Re: Geometrická postupnosť
vyjádři si  pomocí
pomocí  a pak to dosaď i do vyjádření
a pak to dosaď i do vyjádření 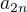 (které se mi zdá poněkud podivné..) a nakonec oba dva takto vyjádřené členy dosaď do zadané rovnosti:
(které se mi zdá poněkud podivné..) a nakonec oba dva takto vyjádřené členy dosaď do zadané rovnosti: 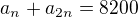 - jediné, co neznáš je
- jediné, co neznáš je  -> dopočítáš -> pomocí něho pak dopočítáš členy
-> dopočítáš -> pomocí něho pak dopočítáš členy  a
a 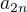
Edit: možná bych si vyjádřil členy takto:  a
a 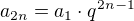
Offline
#3 11. 04. 2010 11:14
Re: Geometrická postupnosť
↑ Doxxik:
Áno, dík moc, teraz je to už jednoduché... ako to, že mi to nenapadlo? :)

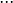
a z toho 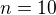
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
