Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 11. 04. 2010 19:35
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: cyklicka zamena
↑ Peter 002:
Přesně, právě jste provedl cyklickou záměnu.
Stručně řečeno, konkr0tní vztah se nevztahuje k pevnému a, b nebo c, ale ke straně určité vlastnosti, přitom její označení může být různé. Například ty Pythagorova věta říká, že druhá mocnina nejdelší strany se rovná součtu... atd. Přitom nejdelší strana může být a, b nebo c. Nebo také q, w ,.. atd.
Takže když použijeme cyklickou záměnu, tak Pythagarova věta může mít podobu:

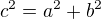
Offline
