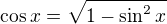Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 04. 2010 18:32
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Goniometrická rovnice
Zdravím nevím si rady s rovnicí  umím jí vyřešit graficky, ale algebraicky jaksi nevim jak na to... Muzete mi nekdo prosim poradit?
umím jí vyřešit graficky, ale algebraicky jaksi nevim jak na to... Muzete mi nekdo prosim poradit?
Offline
- (téma jako vyřešené označil(a) Tychi)
#3 13. 04. 2010 18:39 — Editoval ondrej.hav (13. 04. 2010 18:40)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Goniometrická rovnice
↑ Tychi: Asi to bude desne jednoduchy, ale nemuzu prijit na to jak preveset cos na sin... jedine cos = sin(x+pi/2)... ale to mi asi nepomuze... Kdyz by tam bylo na druhou tak bych vedel... bohuzel v zadani je na prvou
Offline
#5 13. 04. 2010 18:45
#6 13. 04. 2010 19:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Goniometrická rovnice
Zdravím vás,
toto je ovšem neekvivalentní úprava - použila bych převod na poloviční úhel: po úpravě součinový tvar.
po úpravě součinový tvar.
nebo dle metody kolegy Zdeňka, kolegovi děkuji.
Offline
#11 13. 04. 2010 21:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Goniometrická rovnice
↑ DDaili:
Zdravím,
zřejmě máš najit zbývající goniometrické funkce - můžeš použit to, co navrhuje kolegyňka Tychi: , znaménko je třeba zvolit podle kvadrantu, ve kterém je úhel. Zvolíme tedy "minus".
, znaménko je třeba zvolit podle kvadrantu, ve kterém je úhel. Zvolíme tedy "minus".
Téma je ovšem vyřešeno, tak bude lepší si založit vlastní a nové. Děkuji.
Offline