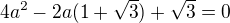Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 03. 2008 11:09 — Editoval ttopi (16. 03. 2008 11:11)
Re: goniometricke rovnice
No protože na jednotkový kružnici je záporný tangens směrem dolů, to znamená, že to co ti vyjde odečti od 360. Alespoň tak to vychází mě. Vyjde nějakejch 271,4° A samozřejmě ro samé 180 - cca 88 ... Pak je to +k krát 180
oo^0 = 1
Offline
#3 16. 03. 2008 11:20 — Editoval jelena (16. 03. 2008 11:30)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricke rovnice
↑ ttopi:↑ liquid:
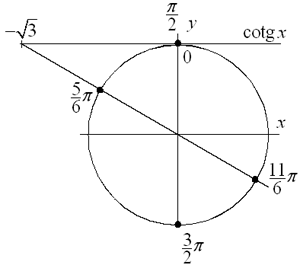
Zaporny tg je ve II. kvadrantu a ve IV. Prvni vysledek by se mel dostat do II. kvadrantu, pak uz staci perioda pro tg x, coz je 180 stupnu, tim se dostaneme do IV. kvadrantu. OK?
Editace: kolega ttopi to ma napsane uplne spravne v editu, kdyz jsem zacala psat sve dve radky, tak to tam jeste nebylo a kdyz jsem to poslala, tak uz jo - ale ja mam mezi tak akorat hrnek kavy :-)
Offline
#10 16. 03. 2008 11:43
Re: goniometricke rovnice
No upravíme do cotgx=pi/4 -> cosx/sinx = pi/4 ... cotg = 1/tg -> tg pi/4 = 0,7853... 1/0,7853 = cca 1,2732... a tan^-1 1,2732 = cca 51,5° ... takže výsledek je cca x=51,5° + k krát 180. Dost nepřesný ale jde o postup.
oo^0 = 1
Offline
#15 16. 03. 2008 12:18
Re: goniometricke rovnice
No jako úhel se pí bere ve spojení s goniometrickou funkcí, to znamená sin(2pí) cos(pí) a podobně. Jinak je jasný, že třeba v negoniometrických rovnicích se pí bere jako hodnota 3,14. To se nějak pozná dycky.
oo^0 = 1
Offline
#16 16. 03. 2008 12:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricke rovnice
↑ liquid:
Budes muset si udelat jasno s cislem pi - jako s realne existujicim cislem na ciselne ose
Moje velmi polopaticka predstava pouziti pi a uhlu ve stupnich:
- koza je uvazana na provazu, delka provazu je 1.
Koza obchazi jednotkovou kruznici.
Budu merit uhlomerem ten uhel od jedne polohy provazu do druhe - merim ve stupnich - a rikam treba "posun proti rucickam o 30 stupnu".
Budu merit svinovacim metrem delku oblouku, co ujde koza na konci provazu, tak merim v radianech a rikam - "posun o pi/6" (radian, ale neni zvykem uvadet jednotky obloukoveho uhlu).
Pokud se bavim o goniometrickych funkcich, tak v podstate mam na mysli porad jednotkovou kruznici - bod se posouva po oblouku, pricemz ten posun muzeme popisovat jak v radianech - pojedeme prstem po oblouku. Tak i ve stupnich - presuneme polomer z jedne polohy na druhou.
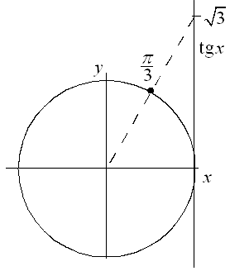
Ted rikam: pri posunu o uhel 30 stupnu, poloha bodu se zmenila o pi/6, bod ma souradnice:
y=sin 30 stupnu = 1/2 ..... nebo sin(pi/6) totez
x = cos 30 stupnu = sqrt(3)/2 nebo sin (pi/6) totez.
Pokud bude zadano, ze cos(uhlu) se rovna pi/4, tak rekli toto - na ose x najdi polohu, kde zhruba bude 3,14/4, a na jednotkove kruznici hledej, o jaky uhel se posunul bod po oblouku. Uhel posunu muze byt jake stupnich, tak i v radianech.
Ovsem neni mozne rici, ze cos(uhlu) se rovna ..... (stupnu).
Dalsi pomucka - cestinarska:
cos čeho? (uhlu at ve stupnich nebo v radianech) = čemu? číslu
Proto nasobek pi muze byt pouzit i na jedne i na druhe strane goniometricke rovnice, stupen pouze po nazvu goniometricke funkce - na obe strany ne.
Offline
#17 16. 03. 2008 13:59
Re: goniometricke rovnice
tohle mi dost pomohlo :)
dekuju :)
mam tu dalsi zadrhelik...
4sin^2x - 2sinx = odmocnina ze 3 * (-1+2 sinx)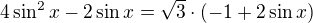
vim jak by se to melo resit, tady mam problem asi v uprave... melo by se to substituovat na kvadr. ale nejak se v tom motam a nejak se mi nepoziraj odmocniny a ani mi nevhychazi vhodne odmocniny ...
Offline
#19 16. 03. 2008 22:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricke rovnice
↑ Ivana:
Ivano, srdecne zdravim :-)
- zadani ma dobre - je z nasi oblibene Petakove, priklad 7b na str 52.
Musi se udelat substituce sin x = a, pak vsechno nalevo, bude kvadraticka rovnice,
4a^2 - a(2+sqrt(3)) + sqrt(3) = 0
Pouze opatrne pri umocnovani na druhou pri hledani D.
Offline
#23 01. 04. 2017 23:22
- Vladimir74
- Zelenáč
- Příspěvky: 1
- Reputace: 1
Re: goniometricke rovnice
↑ jelena:
No, je pěkný, že si přejete hezkej den, ale správnej výpočet je samozřejmě ten, že vytknete 2sinx. Pak se to dá triviálně počítat. Jeden kořen 2sinx=sqr3, druhej 2sinx=1. Doufám, že neučíte matiku, děťátka.
Offline
#24 02. 04. 2017 00:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricke rovnice
↑ Vladimir74:
také Vás zdravím a děkuji za velmi efektivní podnět, skutečně úpravou 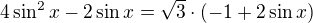 na
na 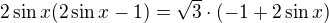 a následně na součinový tvar se dobereme výsledku daleko snadněji a pohodlněji.
a následně na součinový tvar se dobereme výsledku daleko snadněji a pohodlněji.
Doufám, že neučíte matiku, děťátka.
:-) ne, rozhodně ne, strýčku! Jak jste toto téma vůbec našel? Děkuji.
Offline