Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 08. 2007 15:25
Odmocňovanie čísel
Ja mám takú otázku. Nikdy som sa nad tým nezamýšľal no som čítal v istom časopise článok a tam bolo, že odmpcnina zo 4 nie je len 2, ale aj -2.
Je to pravda?; ak áno prečo potom považujeme, aspoň ja som mal vždy dojem, že je jasný výsledok SQRT4, za prirodzene 2?
You know who
(or maybe not)
Offline
#2 27. 08. 2007 17:46 — Editoval Bimetal (27. 08. 2007 17:52)
Re: Odmocňovanie čísel
Jestliže čtverka se dá zapsat jako 2^2, pak odmocnina ze čtyř by měla odpovídat spíše vzorečku 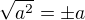 než-li
než-li  , což podporuje ten výsledek ±2. Proč se to ale normálně pro výsledek neuvažuje, to mi hlava nebere, tady můj selský rozum a chatrná středoškolská matemtika končí.
, což podporuje ten výsledek ±2. Proč se to ale normálně pro výsledek neuvažuje, to mi hlava nebere, tady můj selský rozum a chatrná středoškolská matemtika končí.
Offline
#3 27. 08. 2007 20:58 — Editoval jelena (27. 08. 2007 20:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odmocňovanie čísel
Myslim si, ze se tady rozproudi debata:-)
Definice odmocniny rika, ze odmocninou nejakeho nezaporneho cisla a rozumime takove nezaporne cislo b, ktere, pokud bude umocneno prislusnou mocninou, tak dostaneme cislo a.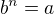 to stejne plati i pro druhou odmocninu
to stejne plati i pro druhou odmocninu 
Logiku to ma, pokud pojimame 2. odmocninu jako inverzni funkci 2. mocniny - ten obrazek urcite znate, tam skutecne x< 0 neni mozne uvazovat.
Tak to nezaporne je OK a odmocnina z 4 by mela byt 2 dle definice (nejlepe obecne zneni "absolutni hodnota z 2").
Neco jineho je, ze pokud nekdo resi rovnici x^2 = 1 a prohlasi, ze ma jeden koren x = 1, tak to je hruba chyba, mensi problem zustane, kdyz napise absolutni hodnota (x) = 1 a pak zapomene, ze x muze byt +1. -1.
Proto i takto zdanlive primitivniho prikladu vyzaduji anulovat pravou stranu a pak x^2 -1 =0, (x-1)*(x+1) = 0 a pak uz je tezke se zmylit, i kdyz :-)
Odmocnovani u rovnic by totiz nebyla ekvivalentni uprava a prave pouziti definice odmocniny by napachalo peknou neplechu. Proto se tomu mame vyhybat s prevest to na upravu ekvivalentni.
Nevim, v jakem smyslu to resil ten clanek, co cetl kolega Matoxy, nebyl by odkaz?
Offline
#4 27. 08. 2007 22:53
Re: Odmocňovanie čísel
Tak jsem se opět ztrapnil tím, že neznám základní definice =))) Holt mám taky ještě kus práce před sebou do maturity z matematiky. Nicméně stejně nechápu, proč se neuvažuje jako výsledek odmocnění absolutní hodnota daného čísla, tak jak je tomu u odmicňování proměnné. Anebo se uvažuje a rovnou se to potom přepíše bez absolutních hodnot a jen nám to ve škole zatajili?
Offline
#5 27. 08. 2007 23:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odmocňovanie čísel
Bimetal napsal(a):
Holt mám taky ještě kus práce před sebou do maturity z matematiky. Nicméně stejně nechápu, proč se neuvažuje jako výsledek odmocnění absolutní hodnota daného čísla, tak jak je tomu u odmicňování proměnné. Anebo se uvažuje a rovnou se to potom přepíše bez absolutních hodnot a jen nám to ve škole zatajili?
Do maturity se toho clovek dovi, neco se dovi i primo u maturity a pak se dovida, a dovida ... hlavne, at ho to bavi :-)
Prave, absolutni hodnota se uvazuje a tak se to rovnou zapise - ale opravdu jen u cisel nebo u pismen - pokud obecne nahrazuji cisla ve VYRAZECH.
V rovnicich je to jinak - mohu provest upravu matematicky spravnou na jedne i na druhe strane rovnice, ale to nemusi mit za nasledek zachovani toho =. No a u nerovnic to je jeste vyznamnejsi.
Tady je dobry material, vesmes je zcela jasny, ale jsou tam i zajimave momenty, treba prave odmocnina http://www.zam.fme.vutbr.cz/~martisek/V … ripta2.pdf
Offline
#6 27. 08. 2007 23:23
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Odmocňovanie čísel
Na netu jsem k tomu našel třeba toto:
http://en.wikipedia.org/wiki/Square_root
Wikipedia napsal(a):
In mathematics, a square root of a number x is a number r such that r2 = x, or in words, a number r whose square (the result of multiplying the number by itself) is x. Every non-negative real number x has a unique non-negative square root, called the principal square root and denoted with a radical symbol as
. For example, the principal square root of 9 is 3, denoted
, because
. The other square root of 9 is −3.
To, že jsou dva pohledy na odmocninu (jeden jako kořen rovnice x^2=t a druháýjako nezáporný reálný kořen této rovnice) zde již bylo zmíněno. Jak vidno, v Angláni pro tyto různé pohledy používají pojmy "square root" a "principal square root". Pokud vím, tak náš termín "odmocnina" opovídá druhému z nich, první bych popsal spojením "komplexní odmocnina". Jakkoli sporné může být slovní označení, je jasné, že "odmocnítkem", tedy symbolem 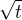 značíme odmocninu, nikoliv komplexní odmocninu.
značíme odmocninu, nikoliv komplexní odmocninu.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 28. 08. 2007 12:03
Re: Odmocňovanie čísel
Bolo to z článku, ktorý bol publikovaný v časopise Quark (neviem či vychádza aj v čechách, ale ak nie tak je to popularizačno-vedecký magazín) na stránke som ten článok nenašiel. Bol to článok o antihmote veta o číslach tam bola len tak okrajovo:
"Matematický dôvod existencie antihmoty je z istého pohľadu celkom jednoduchý: odmocninou z čísla 4 je 2, ale aj -2. A presne takýmto spôsobom, iba znamienkom, sa líšia aj riešenia tzv. Diracovej rovnoce opisujúúcej sprívanie elektrónov a pozitrónov."
You know who
(or maybe not)
Offline
#9 28. 08. 2007 16:41
Re: Odmocňovanie čísel
Ahoj, měla bych dotaz:
Sestroj graf funkce 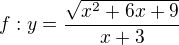 . Autor upravil výraz na zlomek ve tvaru |x+3|/(x+3). Nechápu, proč je v čitateli na absolutní hodnota- když si určím definiční obor, tak přece vyjdou všechna reálná čísla kromě -3, tak proč ten čitatel omezuje? Nebo se to tak musí upravit kvůli nulovým bodům?
. Autor upravil výraz na zlomek ve tvaru |x+3|/(x+3). Nechápu, proč je v čitateli na absolutní hodnota- když si určím definiční obor, tak přece vyjdou všechna reálná čísla kromě -3, tak proč ten čitatel omezuje? Nebo se to tak musí upravit kvůli nulovým bodům?
Offline
#10 28. 08. 2007 18:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odmocňovanie čísel
Pro Autocont:
to je velmi vhodny dotaz k tomu, co zde diskutujeme - autor upravy spravne pouzil definici odmocniny. Provedeou upravou rika, ze pokud odmocnujeme, pak v uvahu mame brat pouze nezaporna cisla, proto je tam absolutni hodnota. Pokud by absolutni hodnotu nepouzil, tak by porusil definici odmocniny.
Co se tyce definicniho oboru - to je v poradku - ma byt vynechano pouze -3 a je to vazano pouze na vyraz v jmenovateli.
Offline
#12 28. 08. 2007 21:37
Re: Odmocňovanie čísel
pro Jelenu:
stejně mi to nedá.
D (f): z definice odmocniny plyne, že výraz pod odmocninou x^2+ 6x+ 9 musí být větší nebo roven 0
(x+3) na 2 je větší nebo rovno 0 ... něco na 2 je vždy větší nebo rovno 0 (takže kromě té -3 je výraz definován pro všechna reálná čísla)
No, a když si pro kontrolu dosadím za x třeba -5, nebo jakékoliv záporné reálné číslo, výraz pod odmocninou je vždy větší než 0, takže je splněna podmínka pro odmocninu. V této fázi teda nechápu, proč je tam ta absolutní hodnota.
Offline
#13 28. 08. 2007 21:48
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Odmocňovanie čísel
autocont: Nebude problém v tom, že jsi minule zapomněl napsat to "na druhou"? Cituji tě: "Autor upravil výraz na zlomek ve tvaru |x+3|/(x+3)" Neupravil ho spíše na  ? Pak by tam ta absolutní hodnota ztrácela význam, protože
? Pak by tam ta absolutní hodnota ztrácela význam, protože 
2+2=4
Offline
#14 28. 08. 2007 21:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odmocňovanie čísel
Pro Autocont:
Srdecne zdravim,
mluvime v podstate spravne, ale o trochu jinych vecich:
- jeden pohled je "definicni obor funkce", kterou mame pred sebou - tam naprosto souhlasim, v zapisu funkce je odmocnina a zlomek, z toho zcela spravne odvozujes definicni obor, tj. lidove receno, jaka cisla smime dosazovat za x a vypocitavat hodnotu funkce.
Dejme tomu, tato funkce popisuje nejaky proces a my skutecne potrebujeme zjistovat hodnoty f(x) pro konkretni x.
- druhy pohled - nebavi nas pracovat s tabulkou, dosazovat x a dopocitavat f(x), potrbujeme si nakreslit graf, bude to nazornejsi. A zjistujeme, ze funkce tak, jak je zadana, by se dala kreslit obtizne. Tak ten zapis budeme upravovat, aby se kreslit dala. A mame moznosti - bud to odmocnit a musime dodrzovat definici odmocniny nebo naopak dostat (x+3) pod odmocninu, pokratit a pak odmocnit. Obe upravy vsak jsou upravy neekvivalentni, tak nam opravdu nic jineho nezbyva, nez kazdou upravu proverit, zda plati nebo ne.
Ostatne, zkus ten graf nakreslit a overit si to vypoctem ruznych hodnot - bude to nazornejsi.
Offline
#15 28. 08. 2007 22:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odmocňovanie čísel
matoxy napsal(a):
"Matematický dôvod existencie antihmoty je z istého pohľadu celkom jednoduchý: odmocninou z čísla 4 je 2, ale aj -2. A presne takýmto spôsobom, iba znamienkom, sa líšia aj riešenia tzv. Diracovej rovnoce opisujúúcej sprívanie elektrónov a pozitrónov."
Stejne pusobive by znelo "Kazde plus ma sve minus", jelikoz to vsechno je predstavou a popisem realneho sveta, ktery ve skutecnosti nezna pojem "odmocnina" ani "pozitron", ale abychm se navzajem v tom svete rozumeli, tak zavadime ruzne definice, vysvetleni a ze nam to jde :-)
Ostatne, jak my si tady v klidu filosofujeme nad odmocninou, budeme myslet pozitivne na rady reparantu, co zitra a pozitri zasednou ke zkouseni. at tu odmocninu, kdyz uz nezdefinuji, tak alespon spocitaji. At jim to vyjde :-)
Offline
#16 28. 08. 2007 22:51
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Odmocňovanie čísel
Lukee napsal(a):
autocont: Nebude problém v tom, že jsi minule zapomněl napsat to "na druhou"? Cituji tě: "Autor upravil výraz na zlomek ve tvaru |x+3|/(x+3)" Neupravil ho spíše na
? Pak by tam ta absolutní hodnota ztrácela význam, protože
tak jsem Autocontův příspěvek první příspěvek vyTeXoval, aby bylo jasné, jaký že to výraz autor upravoval. Autor výraz upravil správně, funce kterou dostal je -1 pro x<3, 1 pro x>3, pro x=3 není definovaná.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#17 26. 01. 2009 15:40
Re: Odmocňovanie čísel
Ahoj,
chtěl bych se zeptat pro jaké číslo může být proměnná n v tomto vzorci ![kopírovat do textarea $\sqrt[n]{a}$](/mathtex/9a/9aa7a9ac54d0c113ac1d436257321e25.gif) , jelikoz si nejsem jistý jestli se nesmí rovnat jen nule, nebo jestli musí být v množině čísel N a nerovnat se nule a nebo musí být ještě ke všemu větší nebo rovno 2, protože prý první odmocnina neexistuje. A pak jestli by to šlo odkaz na nějakou knihu nebo internetovou stránku, kde bych tuto informaci mohl potvrdit.
, jelikoz si nejsem jistý jestli se nesmí rovnat jen nule, nebo jestli musí být v množině čísel N a nerovnat se nule a nebo musí být ještě ke všemu větší nebo rovno 2, protože prý první odmocnina neexistuje. A pak jestli by to šlo odkaz na nějakou knihu nebo internetovou stránku, kde bych tuto informaci mohl potvrdit.
Offline
#18 26. 01. 2009 19:52
Re: Odmocňovanie čísel
n-tá odmocnina z čísla a má význam pro a>=0. Věř mi. Ale kdyby přece http://cs.wikipedia.org/wiki/Odmocnina
Offline
#20 26. 01. 2009 21:39
Re: Odmocňovanie čísel
↑ halogan: no jde o to, že profesorka mi napovídala, že n musí být větší nebo rovno 2 a musí náležet do množiny čísel N, což je podle mně blbost. Ale podle ní, je to prostě nemožné, abych to tak mohl napsat.
Nevíte tedy o nějaké literatuře, kde by byla použita třeba záporná nebo prvá odmocnina ? A ještě dodatek, možná vás zmátla moje přezdívka, ale sem chlap.
Offline
#21 27. 01. 2009 01:11
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Odmocňovanie čísel
↑ Nafido:Jak tu už bylo zmíněno, definice odmocniny je otázkou konvencí. Je fakt, že něco jako půltá odmocnina z a je zbytečné definovat, když to můžeme zapsat jako a^2. Proto se odmocnina často zavádí jen s přirozeným n (http://cs.wikipedia.org/wiki/Odmocnina). Haloganův vzorec platí pro nezáporná reálná a a reálná n kromě 0. Jedná se o vztah mezi mocninnou funkcí a^(1/n) a odmocninou. Dal by se použít k rozšíření definice odmocniny pro všechna reálná (či dokonce komplexní) n kromě 0, což ovšem dělají pouze někteří matematici. Konvence, že přirozené je tedy rozumná.
Že by mělo být n alespoň 2, to slyším dnes poprvé :) Nicméně pokud je to konvence vaší paní profesorky, doporučuji se tím řídit. (Osobně třeba nemám rád tvrzení, že 0 je přirozené číslo -- 0 je naprosto nepřirozená, zeptejte se jakéhokoliv číselného teoretika. Ale jsou i dost schopní vědci s titulem prof., kteří 0 za přirozenou považují ... )
BRKOS - matematický korespondenční seminář pro střední školy
Offline
 ,ale korene rovnice
,ale korene rovnice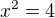 sú
sú aj
aj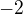 teda
teda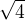 aj
aj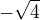
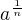 a zkus to vykoumat.
a zkus to vykoumat.